Реферат: Некоторые приложения финансовой математики
Рассмотрим совмещение конверсии (обмена) валюты и наращения простых процентов, сравним результаты от непосредственного размещения имеющихся денежных средств в депозиты или после предварительного обмена на другую валюту. При этом возможны 4 варианта наращения процентов:
- Без конверсии, когда валютные средства размещаются в качестве валютного депозита, наращение первоначальной суммы производится по валютной ставке путём прямого применения формулы простых процентов.
- С конверсией, при это валютные средства конвертируются в тенге, наращение идёт по ставке в тенге, в конце операции сумма в тенге конвертируется обратно в исходную валюту.
- Без конверсии, в этом случае сумма в тенге размещается в виде депозита в тенге, на который начисляются проценты по ставке в тенге по формуле простых процентов.
- С конверсией, когда сумма в тенге конвертируется в какую – либо конкретную валюту и инвестируется в валютный депозит. Проценты начисляются по валютной ставке. Наращенная сумма в конце операции вновь конвертируется в тенге.
Операции без конверсии не представляют сложности. В операции наращения с двойной конверсией имеются два источника дохода: начисление процента и изменение обменного курса. Причём начисление процента является безусловным источником (ставка фиксирована, инфляцию не рассматриваем). Изменение обменного курса может, как быть источником дополнительного дохода, так и приводить к потерям. Остановимся на двух вариантах, предусматривающих двойную конверсию (варианты 2 и 4).
Введём обозначения:
Pv - сумма депозита в валюте,
Pr - сумма депозита в тенге,
Sv – наращенная сумма в валюте,
Sr – наращенная сумма в тенге,
K0 – курс обмена в начале операции,
K1 – курс обмена в конце операции,
n – срок депозита,
i – ставка наращения для тенговых сумм(в виде десятичной дроби),
j - ставка наращения для конкретной валюты.
Рассмотрим варианты:
ВАЛЮТА –> ТЕНГЕ –> ТЕНГЕ –> ВАЛЮТА.
Операция состоит из трёх этапов: обмена валюты на тенге, наращение суммы в тенге, обратное конвертирование суммы в тенге в исходную валюту. Наращенная сумма, получаемая в конце операции в валюте, составит
Sv =Pv K0 (1+ni)/K1
Как видим, три этапа операции нашли своё отражение в этой формуле в виде трёх сомножителей.
Множитель наращения с учётом двойного конвертирования
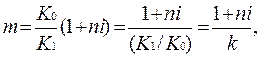
Где k=K1 /K0 – темп роста обменного курса за срок операции. Из данной формулы следует, что множитель наращения m связан линейной зависимостью со ставкой i и обратной – с обменным курсом в конце операции K1 (или с темпом роста обменного курса k).
Исследуем зависимость общей доходности операции с двойной конверсией от соотношения конечного и начального курсов обмена k.
Простая годовая ставка процентов, характеризующая доходность операции,
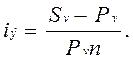
Подставляя в эту формулу выражение для Sv , получаем:
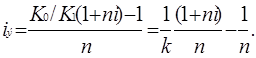
Из этой формулы следует, что с увеличением k доходность iэ падает. При k=1 доходность операции равна ставке в тенге, т.е. iэ =i. Величина iэ < i при k > 1 и iэ > iпри k < 1. При некотором критическом значении k, которое обозначим как k* , доходность операции равна нулю. Из равенства iэ =0 находим:
k* =1+ni,
что означает
K* 1 =K0 (1+ni).
Таким образом, если ожидаемые величины k и K* 1 превышают свои критические значения, то операция убыточна (iэ < 0).
Определим максимально допустимое значение курса обмена в конце операции K1 , при котором эффективность будет равна существующей ставке по депозитам в валюте, и применение двойного конвертирования не даёт никакой дополнительной выгоды. Для этого приравняем множители наращения для двух альтернативных операций
1+nj=(1+ni)K0 /K1
Из полученного равенства следует, что
max K1 =K0 (1+ni)/(1+nj)
или
max k=K1 /K0 =(1+ni)/(1+nj).
Таким образом, депозит валюты через конверсию в тенге выгоднее валютного депозита, если обменный курс в конце операции ожидается меньше max K1 .
Рассмотрим вариант:
ТЕНГЕ –> ВАЛЮТА –> ВАЛЮТА –> ТЕНГЕ.
Это операция с двойной конверсией, когда исходная и конечная суммы в тенге. В этом случае трём этапам операции соответствуют три сомножителя для наращенной суммы:
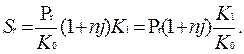
--> ЧИТАТЬ ПОЛНОСТЬЮ <--