Реферат: Некоторые приложения финансовой математики

Пример .

Имеется сумма в евро, которую предполагается разместить на полугодовой депозит. Обменный курс в начале операции 193 тенге за евро, в конце операции предполагается 197 тенге. Годовая ставка простых процентов по депозитам в тенге 17%, по валютным – 5%.

Определить вид наиболее выгодного размещения вклада.

Решение.

Темп роста обменного курса за срок операции

k=K₁ /K₀ =197/193=1,02.

По формуле 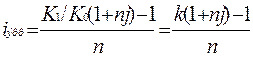имеем:

i_эфф =[1,02^. (1+0,5^. 0,05)-1]/0,5=0,091

Выгоднее разместить депозит в тенге.

Погашение задолженности частями.

Контур финансовой операции – это графическое изображение процесса погашения краткосрочной задолженности частичными (промежуточными) платежами.

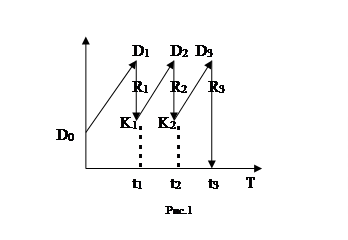
Пусть ссуда в размере D₀ выдана на срок t. На протяжении этого срока в счёт погашения задолженности производятся два промежуточных платежа R₁ и R₂ , а в конце срока выплачивается остаток задолженности R₃ , подводящий баланс операции.

На интервале времени t₁ задолженность возрастает до величины D₁ . В момент t₁ долг уменьшается до величины K₁ =D₁ -R₁ и т. д. Заканчивается операция получением кредитором остатка задолженности R₃ . В этот момент задолженность полностью погашается.

С помощью последовательных частичных платежей иногда погашаются краткосрочные обязательства. В этом случае существуют два метода расчёта процентов и определения остатка задолженности:

1. Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга.

Для случая, показанного на рис.1, получим следующие расчётные формулы для определения остатка задолженности:

K₁ =D₀ (1+t₁ i)-R₁ ; K₂ =K₁ (1+t₂ i)-R₂ ;

K₂ (1+t₃ i)-R₃ =0,

где t₁ , t₂ , t₃ – периоды времени, заданные в годах; i – годовая процентная ставка.

2. Правило торговца.

При общем сроке ссуды t ≤1 можно записать следующее выражение:

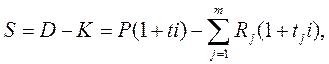
где S – остаток долга на конец срока; D – наращенная сумма долга; K – наращенная сумма платежей; R_j – сумма частичного платежа; t_j – интервал времени от момента платежа до конца срока; m – число частичных (промежуточных) платежей; P – ссуда банка.

Переменная сумма счёта и расчёта процентов.

Рассмотрим ситуацию, когда в банке открыт сберегательный счёт, который изменяется в течение срока хранения: денежные средства снимаются, делаются дополнительные взносы. Тогда в банковской практике при расчёте процентов часто используют методику расчёта с вычислением так называемых процентных чисел. Каждый раз, когда сумма счёта изменяется, вычисляется процентное число С_j за прошедший период j, в течение которого сумма на счёте осталась неизменной, по формуле

C_{j =} P_j t_j / 100,

где t_j – длительность j – го периода в днях, P_j – сумма на вкладе j-го периода.

Для определения суммы процентов, начисленной за весь срок, все процентные числа складываются, и их сумма делится на постоянный делитель D:

D=K/i,

где К – временная база (число дней в году, т.е. 360,365 или 366);

i – годовая ставка простых процентов, %.

При закрытии счёта владелец получит сумму, равную последнему значению суммы на счёте плюс сумма процентов.

Пример.

Вкладчиком 20 января в банке был открыт счёт до востребования в размере Р₁ =1000$, процентная ставка по вкладу составляла i=17% годовых. Дополнительный взнос на счёт составил R₁ =2000$ и был сделан 10 февраля. Снятие со чёта в размере R₂ =1500$ зафиксировано 3 марта. 10 апреля того же года счёт был закрыт.

Определить сумму процентов и общую сумму, полученную вкладчиком при закрытии счёта. При расчётах принять схему 360/360, простые проценты с приближенным числом дней ссуды.

Решение

В задаче имеются 3 периода, в течение которых сумма на счёте оставалась неизменной: с 20 января по 10 февраля (Р₁ =1000$; t₁ =21), с 10 февраля по 3 марта (t₂ =21; P₂ =P₁ +R₁ =1000$+2000$=3000$), с 3 марта по 10 апреля (P₃ =P₂ +R₂ =3000$-1500$=1500$; t₃ =38).