Реферат: Обратное дискретное преобразование Лапласа
Решение: Определяем значения полюсов z1 = 1, их количество n = 1 и кратность m = Используя формулу обратного дискретного преобразования, определяем оригинал

Пример 10. Определить непрерывную функцию, если ее дискретное изображение равно
![]()
Решение: Определяем значения полюсов z1 = d, их количество n = 1 и
кратность m = 1. Используя формулу обратного дискретного преобразования, определяем оригинал

Пример 11. Определить непрерывную функцию, если ее дискретное изображение равно

Решение: Определяем значения полюсов z1 = 1, z2 = d, их количество
n = 2 и кратность m = 1. Используя формулу обратного дискретного преобразования, определяем оригинал

Пример 1 Определить непрерывную функцию, если ее дискретное изображение равно

Решение: Определяем значения полюсов z1 = d их количество n = 1 и кратность m = 1. Используя формулу обратного дискретного преобразования, определяем оригинал
![]()
3. Определение оригинала с помощью разложения на простые дроби
Дискретное изображение можно разложить на простые дроби и, используя табличные значения изображений для каждой составляющей, входящей в разложение, найти оригиналы.
Пример 13. Определить непрерывную функцию, если ее дискретное изображение определяется соотношением
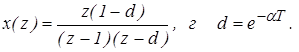
Решение: Представим x(z) в виде простых дробей
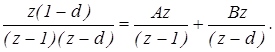
Значения параметров A и B находим методом неопределенных коэффициентов
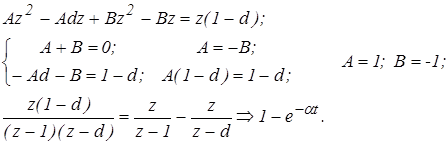
Определение оригинала с помощью разложения дискретного изображения в степенной ряд
Для выхода импульсного элемента можно записать соотношение
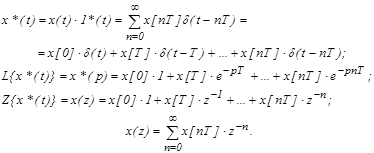
Таким образом, формула прямого дискретного преобразования может быть использована для получения оригинала по изображению, так как x[nT] в формуле прямого дискретного преобразования представляет значения непрерывного сигнала в дискретные моменты времени.
Любая x(z) представляет отношение степенных полиномов.