Реферат: Обратное дискретное преобразование Лапласа
Если это отношение разложить в ряд по степеням z, то коэффициенты при z представляют собой значения оригинала. Дробно – рациональную функцию можно разложить в ряд путем деления числителя на знаменатель или представить в виде суммы простых дробей.
Пример 14. Определить непрерывную функцию, если ее дискретное изображение определяется соотношением
![]()
Решение: Выполняем почленное деление полиномов
 z z-d
z z-d
-z+d 1+dz-1 +d2 z-2 +…+dn z-n
d
-d+d2 z-1
d2 z-1
-d2 z-1 +d3 z-2
d3 z-2
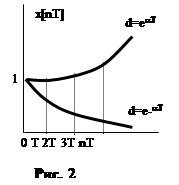
По полученным значениям x[nT] строим график функции приведенный на рис. 2.
Пример 15. Определить непрерывную функцию, если ее дискретное изображение равно

Решение:
Выполняем почленное деление полиномов

 z+1 z2 +z+1
z+1 z2 +z+1
-z-1-z-1 z-1 -z-3 +z-4 -z-6 +z-7
-z-1
-z-1 -z-2 -z-3
z-2 + z-3
-z-2 -z-3 -z-4
-z-4
-z-4 -z-5 -z-6
z-5 +z-6
Рис. 3
По полученным значениям x[nT] строим график функции приведенный на рис. 3.
Для определения решетчатой функции по ее дискретному изображению можно использовать любой из рассмотренных методов. Выбор метода зависит от формы представления изображения.