Реферат: Обратное дискретное преобразование Лапласа

1. Теорема линейности. Изображение линейной комбинации решетчатых функций соответствует линейной комбинации их изображений

(6)

т.е. изображение суммы равно сумме изображений

.

Теорема запаздывания и упреждения (смещения аргументов). Смещение оригинала на ±k соответствует умножению изображения на z^{± k}

(7)

3. Теорема свертывания в вещественной области (умножения изображений)

Для непрерывных систем

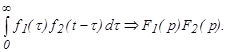(8)

Для дискретных систем

(9)

4. Дуальная теорема. Теорема свертывания в комплексной области (умножения оригиналов)

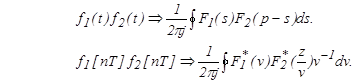(10)

5. Теорема о начальном значении функции

(11)

6. Теорема о конечном значении функции

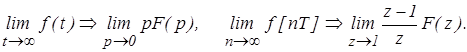(12)

7. Преобразование смешанного изображения в дискретное

(13)

8. Теорема разложения

Если где , то

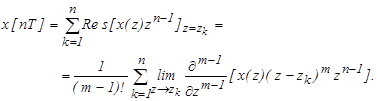(14)

Список литературы

1. Кожевников Н.И., Краснощекова Т.И., Шишкин Н.Е. Ряды и интегралы Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа.-М., Наука, 1964

2. Краснов М.Л., Макаренко Г.И. Операционное исчисление. Устойчивость движения.- М., Наука, 1964.-103 с.

3. Микусинский Я. Операторное исчисление.-М., ИЛ, 1956

4. Сергиенко А.Б. Цифровая обработка сигналов. — 2-е. — Спб: Питер, 2006. — С. 751.

5. Гольденберг Л.М. и др. Цифровая обработка сигналов: Учебное пособие для вузов. - М.: Радио и связь, 1990.- 256 с.