Реферат: Обучаемая система поддержки коллективного решения группы независимых экспертов

решения

P(Ai /V1)

P(Ai /V2) P(Ai /V3)  i A1 0,04 0,01 0,03  1 = 1 A2 0,01 0,03 0,02  2 = 3 A3 0,03 0,05 0,01  3 = 2 A4 0,02 0,02 0,06  4 = 2 A5 0,01 0,05 0,04  5 = 3

Легко видно, что в данном случае частные решения экспертов противоречивы, причем І1={1}, І2={3,4}, І3={2,5}. Для принятия коллективного решения вычислим следующие величины

= 4,03·10-8,

= 1,12·10-6,

= 3,73·10-6.

Поскольку третья из найденных величин максимальна, то, на основании правила (6), принимаем окончательное решение в пользу класса V3.

Частный случай коллективного решения. Рассмотрим одну из типичных задач медицинской диагностики. Требуется отнести обследуемого пациента Z к одному из двух классов: V1 – болен, V2 – здоров на основании результатов двум диагностических тестов A1, A2. При этом будем считать известными априорные вероятности P(V1), P(V2), а эффективность каждого теста, как это принято в медицинской диагностике [19], характеризовать двумя показателями: чувствительностью Qi = 1- P(Ai /V1), где вероятность P(Ai /V1) ошибочного отнесения больного пациента к здоровому и специфичностью Wi = 1- P(Ai /V2), где вероятность P(Ai /V2) ошибочного отнесения здорового пациента к больному.

Ясно, что в результате тестирования возможны четыре комбинации частных решений:

S11: δ1 = 1, δ2 = 1;

S12: δ1 = 1, δ2 = 2;

S21: δ1 = 2, δ2 = 1;

S22: δ1 = 2, δ2 = 2.

Легко видно, что в ситуациях S12 и S21 частные решения противоречивы. Для принятия коллективного решения воспользуемся правилом (6). При этом в ситуации S12, когда A1 признал Z больным, а A2 - здоровым, окончательный диагноз следует ставить согласно схеме:

(7)

где λ = P(V2)/P(V1) – отношение априорных вероятностей здоровых и больных пациентов.

В ситуации же S21, когда A1 признал Z здоровым, а A2 – больным, окончательный диагноз следует ставить согласно схеме:

(8)

Заметим, что для принятия коллективного решения по правилам (6) –(8) требуется весьма ограниченная априорная информация, которая может быть получена на основании предыдущего опыта. При этом совершенно не требуется знать, как именно эксперты принимают частные решения – используя формальный или эвристический алгоритм, либо просто полагаясь на свою интуицию.

В то же время мы сделали одно важное допущение о том, что решения экспертов независимы, которое, естественно, должно быть обоснованно. На практике достаточно веским обоснованием такого допущения может служить знания о том, что частные решения принимаются по статистически независимым данным.

Оценка вероятностных характеристик. Вполне понятно, что при решении практических задач точные значения вероятностных характеристик, фигурирующих в правилах (6)-(8), чаще всего неизвестны. Однако при достаточном объеме наблюдений вероятности P(Vk) и P(Ai / Vk) могут быть оценены соответствующими частотами:

(9)

(10)

где Gk – число появлений k-го класса (k = 1,…M) в выборке из G наблюдений, а Eki – число ошибочных решений i-го эксперта (i = 1,…, N) при анализе ситуаций, когда объект Z принадлежит k-му классу.

Рассмотрим схему оценки частот (9),(10), которая удобна для практического применения и может быть положена в основу системы поддержки принятия коллективного решения. Предположим, что для каждого из G наблюдений известна точная принадлежность Z к одному из возможных классов, выраженная в виде указаний “учителя” y[1], y[2], … , y[G], где y[n]. Запишем частоту появления k-го класса, оцененную согласно (9), в виде

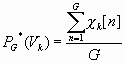(11)

где

Поскольку правую часть (11) можно выразить в виде суммы двух слагаемых