Реферат: Окремі випадки задач оптимального стохастичного керування

· , , , і деякого .

У задачі (4) – (5) може бути уведене додаткове обмеження на стан системи , . У такому разі, якщо , позначатимемо .

3. Оптимальне стохастичне керування: зліченний простір збурень

Розглянемо відображення , що задане формулою

, (6)

за таких припущень:

параметр приймає значення зі зліченної множини з заданим розподілом ймовірностей , що залежать від і ; функції і відображають множину відповідно в множини і , тобто , ; скаляр додатний.

Якщо , , – елементи множини , – довільний розподіл ймовірностей на , а – деяка функція, то математичне сподівання визначається за формулою

,

де ,

,

.

Оскільки , то математичне сподівання визначене для будь-якої функції і будь-якого розподілу ймовірностей на множині .

Зокрема, якщо , ,… – розподіл ймовірностей на множині , то формулу (6) можна переписати так:

При використанні цього співвідношення треба пам’ятати, що для двох функцій , рівність має місце, якщо виконується хоча б одна з трьох умов:

та ;

та ;

та .

Відображення задовольняє припущенню монотонності. Якщо функція – тотожний нуль, тобто , , то за умови , , функцію витрат за кроків можна подати у вигляді:

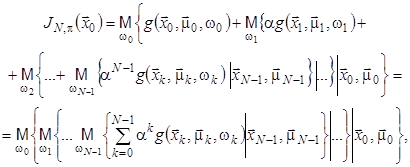(7)

де , .

Ця умова означає, що математичне сподівання обчислюється послідовно по всіх випадкових величинах .

При цьому зміна порядку операцій додавання і узяття математичного сподівання припустима, тому що , , і для довільних простору з мірою , вимірної функції і числа має місце рівність .

Якщо виконується одна з двох нерівностей

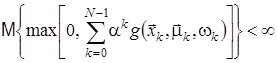або

,

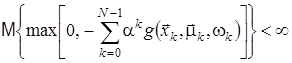то функцію витрат за кроків можна записати у вигляді:

,

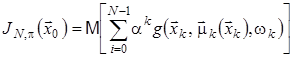де математичне сподівання обчислюється на добутку мір на , а стани , , виражаються через за допомогою рівняння .