Реферат: Определенный интеграл

Из условия задачи следует, что , . По формуле (9) получаем

.

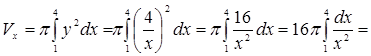
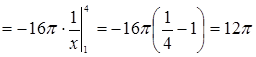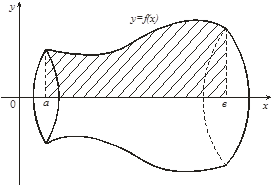
Рис. 10

Рис. 11

Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d , осью Оу и графиком непрерывной на отрезке функции (рис. 12), определяется по формуле

. (10)

х = j ( у )

Рис. 12

Пример 14 . Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х ² = 4у, у = 4, х = 0 (рис. 13).

Решение. В соответствии с условием задачи находим пределы интегрирования: , . По формуле (10) получаем:

.

Рис. 13

3. Длина дуги плоской кривой

Пусть кривая , заданная уравнением , где , лежит в плоскости (рис. 14).

Рис. 14

Определение. Под длиной дуги понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.

Если функция и ее производная непрерывны на отрезке , то длина дуги кривой вычисляется по формуле

. (11)

Пример 15 . Вычислить длину дуги кривой , заключенной между точками, для которых .

Решение. Из условия задачи имеем . По формуле (11) получаем:

.

4. Несобственные интегралы с бесконечными пределами интегрирования

При введении понятия определённого интеграла предполагалось, что выполняются следующие два условия:

а) пределы интегрирования а и являются конечными;