Реферат: Определенный интеграл

Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.

Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.

Определение. Пусть функция определена и непрерывна на промежутке , тогда

(12)

называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).

Если существует и конечен, то несобственный интеграл называется сходящимся ; если данный предел не существует или равен , то несобственный интеграл называется расходящимся .

Геометрически несобственный интеграл от неотрицательной функции выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции , снизу – осью , слева – отрезком прямой и неограниченной справа (рис. 15).

Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.

Рис. 15

Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:

. (13)

Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.

Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:

, (14)

где с – любая точка интервала . Интеграл сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).

Пример 16. Исследовать на сходимость несобственные интегралы:

а) ; б); в) ; г) .

Решение. а) , следовательно, данный интеграл расходится;

б)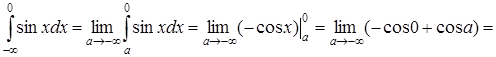

. Так как при предел не существует, то интеграл 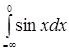расходится;

в)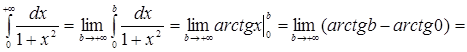

Значит, несобственный интеграл 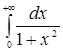сходится и его значение равно ;

г) 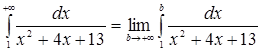= [выделим в знаменателе полный квадрат: ] = [замена:

] =

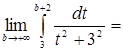
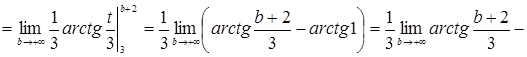
Значит, несобственный интеграл сходится и его значение равно .

5. Несобственные интегралы от неограниченных функций

Пусть функция непрерывна на конечном промежутке , но не ограничена на этом промежутке.