Реферат: Оптимальність у системах керування

1. Умови оптимальності у неавтономних системах керування

У загальному випадку неавтономної системи права частина закону руху й підінтегральна функція цільового функціонала залежать явно від часу , тобто закон руху має вигляд:

, (1)

а цільовий функціонал дорівнює

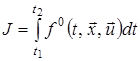. (2)

Тут функції і – неперервні по сукупності змінних і неперервно диференційовані по змінних , , .

Також вважатимемо, що момент часу , який відповідає початковому стану , відомий, а момент часу проходження через кінцеву точку не заданий і повинен бути знайдений, тобто сформульована задача – це задача з вільним часом.

Поставлена задача може бути зведена до автономної задачі введенням додаткової змінної . До закону руху при цьому додається рівняння

,

а до початкових умов – співвідношення .

Тепер систему (2) можна переписати у вигляді:

(3)

а функціонал дорівнюватиме

, (4)

де (відповідно до доданого у початкову систему рівняння).

Отже, неавтономну -вимірну задачу було зведено до автономної задачі з розширеним фазовим простором. У новій задачі потрібно знайти оптимальну траєкторію, що поєднує точку розширеного фазового простору з деякою точкою на прямій, яка проходить через точку паралельно осі . Оскільки кінцеве значення змінної невідоме, то нова задача – це задача з фіксованим лівим і рухомим правим кінцями.

Якщо в задачі оптимального керування (3) – (4) відомі і початковий момент часу й кінцевий момент часу , то задача називається задачею з фіксованим часом. Перетворення цієї задачі введенням додаткового змінного приводить до задачі з фіксованими кінцями в такому формулюванні. Потрібно знайти керування , що переводить фазову точку системи (2) зі стану в момент часу у стан в момент часу , причому функціонал (4) набуває найменшого значення. Зауважимо, що момент часу попадання в точку можна не вважати фіксованим, оскільки в силу тотожності попадання в точку може відбутися тільки в цей момент часу. Таким чином, до даної задачі можна застосувати теорему, відповідно до якої для одержання необхідних умов екстремуму функціонала необхідно максимізувати функцію Понтрягіна

, (5)

де – загальний вигляд функції Понтрягіна з теореми 1, у якій не врахована додаткова, ()-ша змінна. Спряжена система для цієї задачі за умов набуває вигляду:

(6)

Має місце така теорема.

Припустимо, , – оптимальний процес для задачі з фіксованим часом. Тоді існує ненульова вектор-функція , що відповідає цьому процесу, така що:

1. Для будь-якого функція змінної набуває максимального значення в точці , тобто:

: .

2. , .

Оскільки, як і раніше, , то умову 2 цієї теореми достатньо перевірити в якій-небудь одній точці відрізка .

Розглянемо випадок, коли при фіксованому правий кінець вільний. Ця задача полягає в тому, щоб із заданого стану за заданий час пройти по траєкторії з довільним кінцевим станом за умови мінімізації цільового функціонала. Умови трансверсальності для цієї задачі набувають вигляду:

, . (7)

Для цього випадку необхідна умова оптимальності полягає в тому, щоб функція досягала максимального значення для кожного на оптимальному керуванні і мала місце умова (7).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--