Реферат: Оптимальність у системах керування

На практиці часто зустрічаються задачі оптимального керування, у яких функція Понтрягіна лінійно залежить від всіх керувань або від частини з них (наприклад, в лінійних задачах оптимальної швидкодії). Однак у нелінійних задачах оптимального керування (якщо функція Понтрягіна є нелінійною по одній або декількох фазових змінних) можлива ситуація, коли на оптимальній траєкторії коефіцієнт при одній з компонент вектора керування обертається на нуль всюди на деякому інтервалі часу, і тоді умова максимуму функції за не дозволяє однозначно визначити оптимальне керування. Ця ситуація називається особливим режимом керування. Дослідимо її детальніше.

Розглянемо автономну задачу оптимального керування

,

Де; , , , ,

– довільна множина з ;

– лінійний простір кусково-неперервних на функцій.

Крайові умови задачі мають вигляд:

, .

Потрібно знайти таке припустиме керування , що переводить систему зі стану у стан , причому відповідний припустимий процес доставляє мінімальне значення функціоналу

,

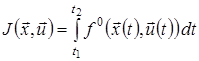де функції , неперервні по сукупності всіх змінних і неперервно-диференційовані по змінних .

Вважатимемо, що функція Понтрягіна для цієї задачі є лінійною за частиною компонент вектора . Виділимо із цих компонент групу з керувань (з тих, за якими функція лінійна) і позначимо їх через , а інші керувань зберемо у вектор (він також може включати компоненти, за якими функція лінійна). За таких умов закон руху набуває вигляду:

,

де .

Складемо функцію Понтрягіна для даної задачі:

.

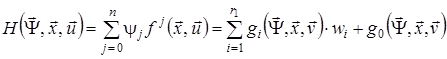Очевидно, що

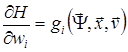, . (8)

Припустимо, що процес разом з розв’язком спряженої системи

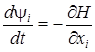, , (9)

задовольняє принципу максимуму і, крім того, припустимо, що у всіх точках деякого інтервалу має місце рівність

, (10)

або, враховуючи (10),

, , . (11)

Ця ситуація означає, що коефіцієнти при на деякому часовому відрізку дорівнюють 0, і оптимальне керування визначити неможливо. У цьому випадку вектор керувань називається особливим керуванням на відрізку , процес – особливим режимом, траєкторія – траєкторією особливого режиму, а відрізок часу – ділянкою особливого керування.

З формули (11) випливає, що на ділянці особливого режиму функція Понтрягіна не залежить від . Дійсно, :

.

Тому в даній ситуації умова максимуму по не дає жодної інформації про конкретні значення керувань .

Оскільки на ділянці особливого режиму має місце співвідношення (11), то очевидно, що