Реферат: Оптимальність у системах керування

Керування називається екстремальним керуванням, якщо воно задовольняє принципу максимуму.

Для лінійної задачі оптимальної швидкодії з областю керування – багатогранником керування є екстремальним, якщо існує таке нетривіальне розв’язання системи (17), для якого матиме місце співвідношення (18).

Зрозуміло, що будь-яке оптимальне керування є екстремальним. Тому, щоб знайти оптимальне керування, що переводить фазову точку зі стану у стан , треба відшукати всі екстремальні керування з цими крайовими умовами, а потім серед них вибрати те, що здійснює перехід за найменший час.

У загальному випадку можуть існувати кілька оптимальних керувань, що переводять фазову точку зі стану у стан , але якщо початок координат у просторі керувань є внутрішньою точкою багатогранника , то екстремальне керування єдине. Отже, у лінійних задачах оптимальної швидкодії принцип максимуму дозволяє не тільки визначити вид оптимальних керувань, але й одержати умови єдиності оптимального керування.

Припустимо, що початок координат є внутрішньою точкою багатогранника припустимих керувань. Якщо і – два екстремальних керування, що переводять фазову точку зі стану у стан за час і відповідно, то і , .

У теоремі має місце умова .

Теорема. Якщо існує хоча б одне керування, що переводить систему (17) зі стану у стан , то існує й оптимальне по швидкодії керування, що також переводить систему з у .

4. Умови оптимальності у задачі з рухомими кінцями

У задачі з рухомими кінцями або початковий стан , або кінцевий стан , або обидва ці стани невідомі. Задані тільки множини і , що містять точки та .

Гіперповерхня – це множина всіх точок , які задовольняють співвідношенню

,

де – скалярна диференційована функція. Якщо – лінійна функція, то гіперповерхня називається гіперплощиною і описується рівнянням

. (19)

Якщо , то гіперплощина (19) є ()-вимірним лінійним підпростором в .

Будь-який ()-вимірний підпростір може бути заданий як множина розв’язань лінійної однорідної системи з рівнянь із невідомими, матриця якої має ранг :

.

Такий лінійний підпростір називається -вимірною площиною. Множина розв’язань системи нелінійних рівнянь

де функції , …, диференційовані і ранг матриці Якобі цієї системи функцій дорівнює , є -вимірним гладким різноманіттям.

Задача оптимального керування з рухомими кінцями полягає в тому, щоб знайти таке припустиме керування для системи із законом руху

, , ,

яке переводить фазову точку з деякого, заздалегідь невідомого, стану на -вимірному різноманітті () у деякий стан на -вимірному різноманітті () і надає найменшого значення функціоналу

.

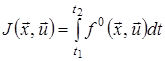Задача оптимального керування з фіксованими кінцями є окремим випадком цієї задачі при , тобто коли різноманіття і вироджуються в точку.

Відсутність рівнянь, що задають початковий і кінцевий стани, приводить до того, що система необхідних умов перестає бути повною. У цьому разі для одержання відсутніх рівнянь використовують умови, що називаються умовами трансверсальності.

Умови трансверсальності. Вектор спряжених змінних із принципу максимуму задовольняє умові трансверсальності на лівому кінці траєкторії , якщо вектор ортогональний дотичній площини до різноманіття в точці , тобто

, (20)

де – довільний вектор, що лежить у дотичній площини. Аналогічно формулюється умова на правому кінці.

Якщо , – оптимальний процес у задачі з рухомими кінцями , , то ненульова вектор-функція , що існує відповідно до теореми 3, задовольняє на кожному з кінців траєкторії умовам трансверсальності.