Реферат: Оптимальність у системах керування

і т.д. Останні співвідношення разом з умовою (10) дозволяють визначити всі особливі режими.

3. Лінійна задача оптимальної швидкодії

Розглянемо лінійну задачу оптимальної швидкодії:

, , (12)

де , ,

, – числові матриці розмірності та відповідно.

Область керування задачі – замкнутий обмежений багатогранник в :

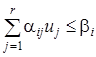, , (13)

Якщо для будь-якого вектора , паралельного будь-якому ребру багатогранника , система векторів, , …, (14)є лінійно незалежною, то багатогранник задовольняє умові спільності положення відносно системи (14).

Для перевірки лінійної незалежності векторів (13) достатньо перевірити, чи матриця, стовпцями якої є стовпці (12), є невиродженою, тобто

.

Перепишемо формулу (10):

, ,

де , – -і рядки матриць і .

Функція Понтрягіна лінійної задачі оптимальної швидкодії має вигляд:

(15)

Оскільки перший доданок у формулі (15) не залежить від , то функція досягає максимуму за змінною одночасно з функцією

.

Спряжена система у цьому випадку може бути записана у вигляді:

, ,

або у векторній формі

. (16)

Позначимо через . З теореми 2 випливає, що якщо – оптимальне керування, то існує такий ненульовий розв’язок системи (16), для якого в кожний момент часу функція набуватиме максимального значення за змінною :

. (17)

Оскільки система (17) з постійними коефіцієнтами не містить невідомих функцій і , то всі її розв’язки можна легко знайти, після чого, використовуючи їх для розв’язання задачі максимізації функції на множині , знаходимо оптимальні керування .

Для будь-якого нетривіального розв’язання системи (11) співвідношення (14) однозначно визначає керування , причому це керування кусково стале, а значеннями керування в точках неперервності є вершини багатогранника .

Точки розриву оптимальної функції керування відповідають зміні значення керування і називаються точками перемикання. Якщо – точка перемикання, то ліворуч від неї керування має одне значення, наприклад, , а праворуч інше – .

Позначимо через підмножину у виду

. (18)