Реферат: Оптимизационные модели принятия решений
После ответа на данные вопросы для построения модели остается только идентифицировать переменные и представить цель и ограничения в виде математических функций этих переменных.
Надлежащий анализ вопросов подобного рода и корректная формулировка математической модели являются центральным звеном решения задач линейной (и не только линейной) оптимизации.
Эффективным средством решения задач линейной оптимизации является MS Excel. Входящий в состав данного программного продукта пакет Поиск решения (Solver) позволяет проводить решения задач подобного рода с большим (свыше 200) числом переменных и ограничений.
Отметим, что применительно к задачам оптимизации производственной программы предприятия наиболее типичными задачами линейной оптимизации являются оптимизация дохода, прибыли, себестоимости, номенклатуры производимой продукции, затрат станочного времени и т.п.
Рассмотрим использование информационных технологий решения задач линейной оптимизации на ряде конкретных примеров, имеющих непосредственное отношение к практике принятия управленческих решений.
Пример 1. Определение оптимального ассортимента продукции
Предприятие изготавливает два вида продукции П1 и П2 , которая поступает в оптовую продажу. Для производства используются два вида сырья ![]() и
и ![]() . Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции приведен в таблице.
. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции приведен в таблице.
Таблица 2.1
| Сырье | Расход сырья на единицупродукции | Запас сырья, ед. | |
| П1 | П2 | ||
| 2 | 3 | 9 | |
| 3 | 2 | 13 | |
Маркетинговые исследования показали, что суточный спрос на продукцию П1 не превышает спрос на продукцию П2 более чем на
1 ед. Кроме того, известно, что спрос на продукцию П2 не превышает 2 единиц в сутки.
Оптовые цены единицы продукции равны для П1 3 д.е., для
П2- 4 д.е. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
Решение
Очевидно, фирме требуется определить объемы производства каждого вида продукции в тоннах, максимизирующие доход в д.е. от реализации продукции, с учетом ограничений на спрос и расход исходных продуктов. Предположим, что предприятие изготовит ![]() единиц продукции П1 и
единиц продукции П1 и ![]() единиц продукции П2. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, получим следующую систему ограничений
единиц продукции П2. Поскольку производство продукции ограничено имеющимся в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию, а также учитывая, что количество изготовляемых изделий не может быть отрицательным, получим следующую систему ограничений
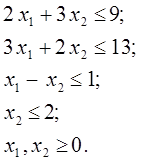
Доход от реализации продукции (целевая функция) составит
![]()
Таким образом, данная простая задача сводится к максимизации целевой функции ![]() при учете вышеприведенных ограничений.
при учете вышеприведенных ограничений.
Проведем решение задачи в Excel.
Введем данные на рабочий лист так, как показано на Рис 2.1.
Искомые значения переменных ![]() будут располагаться в ячейках A10 и B10 соответственно, целевая функция – в ячейке E10.
будут располагаться в ячейках A10 и B10 соответственно, целевая функция – в ячейке E10.
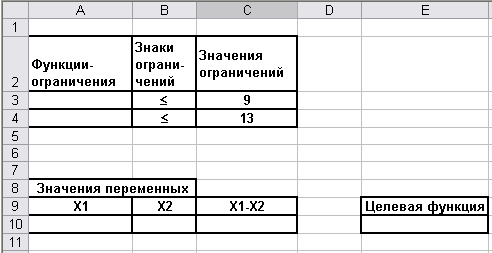
Рис. 2.1
В ячейки A3, A4 введем левые части функций – ограничений: =2*A10+3*B10 и = 3*A10+2*B10 соответственно. В ячейку C10 введем левую часть третьей функции-ограничения: =A10-B10.
Далее, запускаем пакет Поиск решения (Сервис ® Поиск решения) и устанавливаем целевую и изменяемые ячейки, а также вводим необходимые ограничения (Рис.2.2)
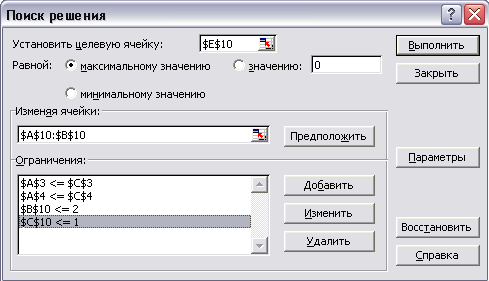
Рис. 2.2 Окно диалога Поиск решения
Поиск решения дает ответ
![]()
![]()
Пример 2 .Использование мощностей оборудования
Предприятие имеет ![]() моделей машин различных мощностей. Задан план по времени и номенклатуре:
моделей машин различных мощностей. Задан план по времени и номенклатуре: ![]() - время работы каждой машины; продукции
- время работы каждой машины; продукции ![]() - го вида должно быть выпущено не менее
- го вида должно быть выпущено не менее ![]() единиц.
единиц.