Реферат: Оптимизационные модели принятия решений

де - искомые координаты обслуживающего клиентов объекта, - координаты -го обслуживаемого объекта, - заданные коэффициенты, характеризующие, например, объемы заказов, или удельную (в расчете на 1 км.) стоимость доставки из соответствующих объектов. Отметим, что в данной задаче не используются ограничения положительности .

Решение проведем для трех случаев, соответствующих 1) отсутствию каких-либо ограничений на координаты , 2) необходимости размещения обслуживающего объекта на некотором прямолинейном отрезке (например, объект может быть расположен лишь на отдельном небольшом участке улицы), 3) расположению объекта в пределах некоторого круга заданного радиуса. Ограничимся случаем трех обслуживаемых объектов .

Первый случай. Отсутствуют какие-либо ограничения на координаты .

Решение

Введем данные на рабочий лист в соответствии с приводимым ниже рисунком.

В качестве изменяемых ячеек выберем B10, B11; в качестве целевой ячейки - ячейку E11 и введем в нее формулу

=J6*КОРЕНЬ((B10-A6)^2+(B11-B6)^2)+K6*КОРЕНЬ((B10-D6)^2+(B11-E6)^2)+L6*КОРЕНЬ((B10-G6)^2+(B11-H6)^2).

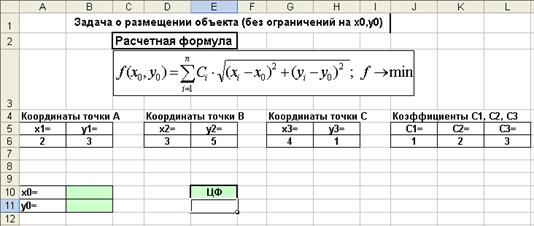
Рис. 2.8 Данные для решения задачи о расположении объекта (без ограничений)

Решение задачи с помощью Поиска решения при заданных координатах точек дает оптимальное значение целевой функции составляет 11,0746.

Второй случай. Координаты принадлежат некоторому отрезку прямой линии, задаваемой уравнением

(в данном примере мы используем значения ).

Решение

Введем данные на рабочий лист в соответствии с приводимым ниже рисунком.

Очевидно, формула для целевой функции (ячейка E12) остается неизменной.

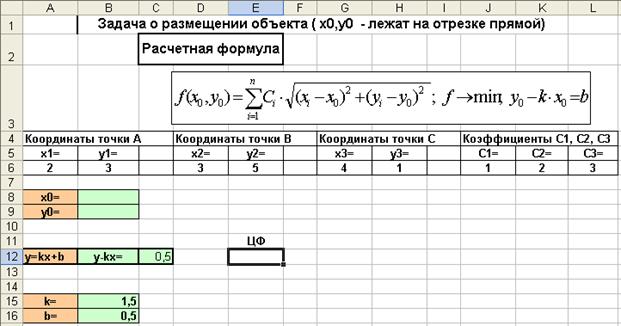
Рис. 2.9 Данные для решения задачи о расположении объекта (координаты объекта лежат на отрезке прямой линии)

Единственным отличием от предыдущего случая является необходимость ввода дополнительного ограничения в ячейку B13; в ячейку B13 вводится формула =B9-B15*B8 и в окне диалога Поиск решения вводится ограничение $B$13=$B$16.

Ответ

оптимальное значение целевой функции составляет 13,6843

Третий случай. Координаты лежат внутри некоторой окружности радиуса (мы полагаем ). Данный случай может соответствовать, например, ситуации, когда необходимо разместить объект вблизи некоторого населенного пункта.

Решение

Введем данные на рабочий лист в соответствии с приводимым ниже рисунком.

Рис. 2.10 Данные для решения задачи о расположении объекта (координаты объекта локализованы в пределах круга определенного радиуса)

Целевая функция располагается в ячейке E11, искомые координаты объекта будут располагаться в ячейках B7, B8. В ячейку B12 введем функцию = B7^2+B8^2. Введем ограничение $B$12<=$C$11, учитывающее то обстоятельство, что объект не должен располагаться вне круга заданного радиуса. Поиск решения дает ответ целевая функция .

Пример 8. Формирование оптимального портфеля ценных бумаг

Требуется сформировать портфель минимального риска из двух видов ценных бумаг – “АРТ” с эффективностью 12% и риском 21,1 и “ВЕРМ” с эффективностью 5,1% и риском 8,3 при условии, что обеспечивается доходность портфеля не менее 8,9%. Коэффициент корреляции равен 0,18.