Реферат: Основи гідравліки

або

.

(2.2)

Середній гідростатичний тиск, який діє на площі w, визначають за формулою:

.

(2.3)

Одиницею тиску в системі СІ є паскаль (1Па=Н/м² ).

Гідростатичний тиск характеризується трьома властивостями.

1. Гідростатичний тиск завжди напрямлений по внутрішній нормалі до поверхні, на яку він діє, і створює тільки стискуючі напруження.

Ця властивість безпосередньо виходить із визначення тиску, як напруження від нормальної стискуючої сили.

2. В будь-якій точці рідини гідростатичний тиск однаковий по всім напрямам.

Щоб довести це виділимо в об’ємі рідини призму з основою у вигляді трикутника АВС (рис 2.2а) і замінимо дію зовнішнього об’єму рідини на її бокові грані відповідними силами. Оскільки призма знаходиться у стані рівноваги, то трикутник цих сил повинен бути замкнутим (рис 2.2б).

Силовий трикутник подібний трикутнику АВС і тому . Якщо поділити всі члени даного рівняння на довжину призми Dl, то в знаменниках будуть стояти площі відповідних граней призми. При спрямуванні розмірів призми до нуля у відповідності з рівнянням 2.1 отримаємо:

РАВ =РВС =РАС =P,

(2.4)

що і потрібно було довести.

3. Гідростатичний тиск в точці залежить тільки від її положення у просторі, тобто р=f(x,y,z).

Цей висновок виходить з викладеного вище.

2.2 Диференціальні рівняння рівноваги рідини

Виділимо в нерухомій рідині нескінченно малий об’єм у вигляді паралелепіпеда з ребрами dx, dy, dz (рис 2.3). Подумки відкинемо рідину, що оточує паралелепіпед, і замінимо її дію відповідними силами. Припустимо, що на ліву грань діє тиск р. Тоді на праву грань А₁ В₁ С₁ D₁ , яка знаходиться на відстанні x+dx, буде діяти тиск .

Відповідно, сила тиску на ліву грань АВСD буде дорівнювати

,

а на праву

(

Рис.2.3

Знак (-) показує, що сила діє у від’ємному напрямі осі х)

Крім сили тиску на паралелепіпед може діяти рівнодіюча масових сил (тяжіння, відцентрова, інерції), проекція якої на вісь х буде:

,

де Х-проекція прискорення (одиничної масової сили) на вісь х;

dV-об’єм паралелепіпеда.

Рівняння рівноваги сил, що діють на паралелепіпед в напрямі осі х, має вигляд:

чи, після спрощень,

Аналогічно можна отримати рівняння рівноваги сил відносно осей y і z

Таким чином, кінцево маємо систему:

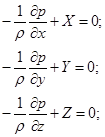(2.5)

Рівняння (2.5) є основними диференціальними рівняннями рівноваги рідини (рівняння Ейлера).

Щоб привести рівняння Ейлера до вигляду, зручного для інтегрування, помножимо кожне з рівнянь (2.5) відповідно на dx, dy, dz і складемо їх почленно:

Ліва частина цього рівняння є повним диференціалом тиску dp, тому:

(2.6)