Реферат: Первичная статистическая обработка информации
{
Рис.1.
2.5. Статистический ряд распределения строится на базе сгруппированного ряда. Для этого вычисляются частоты попадания значений x в соответствующие разряды по формуле:
Статистический ряд распределения представлен в таблице 4.
Таблица 4
|
Разряды
| [280..320] | (320..360] | (360..400] | (400..440] | (440..480] | (480..520] |
|
Частоты
| 0.02 | 0.10 | 0.36 | 0.33 | 0.14 | 0.05 |
2.6. Графической иллюстрацией статистического ряда распределения является “полигон частот”, представленный на рис.2.
Рис.2.
2.7. Статистический ряд распределения является основой для вычисления и построения эмпирической плотности вероятности (рис.3). Гистограмма строится в виде прямоугольников, основания которых равны длинам разрядов, а высоты определяются из соотношения:
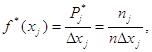
где 
длина j -го разряда (j=1..m ).
Результаты расчетов по оценке эмпирической плотности вероятности 
приведены в таблице 5, а гистограмма на рис.3. (dx = 40)
Таблица 5
|
Разряды
| [280..320] | (320..360] | (360..400] | (400..440] | (440..480] | (480..520] |
|
Значения
| 0.050 | 0.250 | 0.900 | 0.825 | 0.350 | 0.125 |
Рис.3.
3. Выполнение второго задания.
3.1. Вычислим точечные и интервальные оценки математического ожидания (выборочного среднего значения) и дисперсии (выборочной исправленной дисперсии) по данным таблиц 1 и 2. сначала определим точечные оценки.
Интервальную оценку математического ожидания (доверительный интервал) при заданной доверительной вероятности (надежности) 
и числе наблюдений (объеме выборки) n =100 определим по формуле:
,