Реферат: Понятие статистики 2

Виды показателей вариации 5-1

Различие индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака .

Показатели вариации характеризуют колеблемость отдельных значений, степень их близости к средней.

Показатель	Простые	Взвешенные
			Абсолютные	Размах вариации	R = xmax - xmin
Среднее линейное отклонение
				Дисперсия
Среднеквадратическое отклонение
				Относительные	Коэф-т осцилляции
Коэф-т линейной вариации
Коэф-т вариации

Если >33%, то это говорит о том, что колеблемость признака в совокупности значительна, совокупность неоднородна, а средняя не является представительной.

Свойства дисперсии 5-2

1. Дисперсия постоянной величины равна нулю

2. Если у всех значений вариант отнять постоянное число А (А=const), то средний квадрат отклонений (дисперсия) не изменится

3. Если все значения вариант разделить на постоянное число А (А=const), то средний квадрат отклонений (дисперсия) уменьшится в А² раз

Дисперсия альтернативного признака 5-3

Альтернативные признаки – это признаки, которые могут принимать только два взаимоисключающих значения.

Наличие признака обозначается 1, а доля единиц совокупности, обладающих данным признаком, обозначается р .

Отсутствие признака обозначается 0, а доля единиц, не обладающих данным признаком, - q .

Очевидно, p + q =1 .

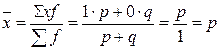
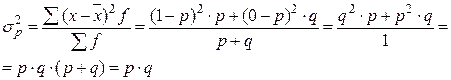
т.е.

Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, и доли единиц, не обладающих им.

5-4

Виды дисперсий в совокупности, разделенной на части

Если изучаемая совокупность подразделена на группы, однородные по изучаемому признаку, то можно исчислить следующие виды дисперсий :

· Внутригрупповые дисперсии (, … ), отражают дисперсию внутри каждой из выделенных групп под влиянием случайной вариации (т.е. части вариации, происходящей под влиянием неучтенных факторов и не зависящей от признака-фактора, положенного в основание группировки).

· Средняя из внутригрупповых дисперсий () – это средняя арифметическая взвешенная из внутригрупповых дисперсий.

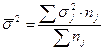
где

- численность выделенных групп

· Межгрупповая дисперсия () – это средний квадрат отклонений групповых средних от общей средней. Характеризует систематическую вариацию, т.е. различия в величине изучаемого (результативного) признака за счет признака-фактора, положенного в основание группировки.

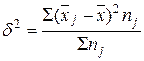
где

- внутригрупповые средние

- общая средняя, которую можно исчислить двумя способами:

1) как среднюю арифметическую взвешенную из внутригрупповых средних: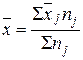

2) обычным способом по данным всей совокупности

· Общая дисперсия () характеризует вариацию признака, которая зависит от всех условий в данной совокупности. Общую дисперсию, так же как и общую среднюю, можно исчислить двумя способами:

1) поправилу сложения дисперсий