Реферат: Посадки с гарантированным натягом

Рисунок 6 – Расчётная схема соединения с натягом

Рассмотрим соединение с натягом дета­лей 1 (в соответствии с рисунком 23) и 2 при действии сдвигаю­щей силы, например, осевой F_а . Взаимное смещение деталей в соединении ограниче­но деформациями за счет сил сцепления, которые возникают благодаря контактным напряжениям q от натяга.

Если принять, что отнесенная к площади контакта сила трения τ пропорциональна контактному напряжению q между сопря­женными деталями, то

где f - коэффициент трения.

Условие взаимной неподвижности дета­лей соединения при действии сдвигаю­щей нагрузки примет вид

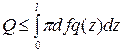
где d и l - диаметр и длина посадочной поверхности.

Введем в рассмотрение номинальные контактные напряжения

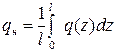; тогда

Из неравенства следует, что нагрузочная способность соединения определя­ется номинальными контактными напряжениями и состоянием контактирующих поверхностей. Напряжения зависят от натяга в соединении и условий работы.

Детали соединения будут взаимно не­подвижными, если средние контактные на­пряжения

где k - коэффициент запаса сцепления, учитывающий возможное рассеяние значе­ний коэффициентов трения, погрешности в форме контактирующих поверхностей и изгиб деталей, ослаб­ляющие их сцепление.

Для соединений, подверженных изгибу, например, соединений валов и зубчатых колес редукторов, принимают значение k= 3,0?4,5,понижая таким образом склонность соединений к фреттинг-корро­зии. В остальных случаях k= I,5?2,0.Значение коэффициента сцепления в формуле следует принимать минимальным из или устанавливать экспериментально.

Нагрузочная способность соединения может быть увеличена также за счет повы­шения коэффициента трениямежду деталями. Эффективным оказы­вается осаждение на поверхности вала тон­кого слоя из частиц карбида бора В₄ С или карбида кремния SiC. Такой слой повышает коэф­фициент трения в соединении с натягом до 0,7 благодаря эффекту микрозацепле­ния и, как следствие, в несколько раз увеличи­вает нагрузочную способность соединения при неизменном натяге.

Рисунок 7 – Внешние силы действующие на соединение

Сдвигающая силаможет быть осевой, т. е.

или окружной (тангенциальной), т. е.

При совместном действии осевой силы и вращающего момента принимают

Уравнение выражает связь внеш­них и внутренних силовых факторов. Для решения задачи следует выразить контакт­ные напряжения через смещения точек деталей.

Условие совместности пере­мещений сопряженных деталей. Предположим, что охватывающая деталь 2 запрессована на охватываемую деталь 1. Тогда в резуль­тате деформации точки поверхностей де­талей 1 и 2 получат радиальные перемещенияu₁ и u₂ , а радиальный натяг δ будет скомпенсирован этими перемеще­ниями, т. е.

где Δ = d_В - d_А - диаметральный натяг деталей.

Уравнение отражает геометричес­кую сторону задачи. Для ее решения необходимо выразить смещения в уравне­нии через контактные напряжения.

Связь смещений и контакт­ных напряжений в соединении. Контактные напряжения q в общем случае распределены по длине соединения существенно неравномерно, так как равномерной деформации препятствуют выступающие части деталей. Связь смещений и контактных давлений имеет вид

где - функция влияния, показы­вающая перемещение точек контакта в сечении z = с от единичной радиальной силы, приложенной в сечении z= ζ; i= 1; 2 - номер детали.

Значения функции λ можно получить расчетом.

В предварительном расчете полагают, что контактные напряжения одинаковы во всех точках поверхностей контакта. Это экви­валентно допущению о сопряжении двух цилиндров одинако­вой длины.

Рисунок 8 – Расчётная схема соединения с натягом

Задача о сопряжении с натягом двух толстостенных цилиндров бесконечной длины рассмотрена в сопротивлении ма­териалов. Установлено, что радиальные перемещения точек кон­такта

;