Реферат: Поверхневі інтеграли
Якщо у формулі (2) покласти ![]() на поверхні
на поверхні ![]() , то отримаємо
, то отримаємо
![]() ,(5)
,(5)
де ![]() – площа поверхні
– площа поверхні ![]() , тобто за допомогою поверхневого інтеграла першого роду можна обчислювати площі поверхонь.
, тобто за допомогою поверхневого інтеграла першого роду можна обчислювати площі поверхонь.
Крім того, поверхневі інтеграли першого роду застосовують при обчисленні маси, координат центра маси, моменту інерції матеріальної поверхні з відомою поверхневою густиною розподілу маси. Виведення відповідних формул по суті не відрізняється від виводу аналогічних формул для матеріальної пластинки.
Якщо на кусково-гладкій поверхні ![]() розподілено масу з поверхневою густиною
розподілено масу з поверхневою густиною ![]() , то:
, то:
а) маса матеріальної поверхні
![]() ;
;
б) координати центра маси поверхні:
![]() ,
,
де ![]() – статичні моменти поверхні
– статичні моменти поверхні ![]() відносно осей
відносно осей ![]() ;
;
в) моменти інерції поверхні відносно осей координат і початку координат:
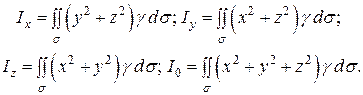
2. Поверхневі інтеграли другого роду
Введемо поняття сторони поверхні. Візьмемо на гладкій поверхні ![]() довільну точку
довільну точку ![]() , проведемо в ній нормаль
, проведемо в ній нормаль ![]() певного напряму і розглянемо на поверхні
певного напряму і розглянемо на поверхні ![]() довільний замкнений контур, який виходить з точки
довільний замкнений контур, який виходить з точки ![]() і повертається в точку
і повертається в точку ![]() , не перетинаючи при цьому межі поверхні
, не перетинаючи при цьому межі поверхні ![]() . Переміщатимемо точку
. Переміщатимемо точку ![]() по замкненому контуру разом з вектором
по замкненому контуру разом з вектором ![]() так, щоб вектор
так, щоб вектор ![]() весь час залишався нормальним до
весь час залишався нормальним до ![]() . При обході заданого контуру ми можемо повернутися в точку
. При обході заданого контуру ми можемо повернутися в точку ![]() з тим самим або з протилежним напрямом нормалі.
з тим самим або з протилежним напрямом нормалі.
Якщо у довільну точку ![]() поверхні
поверхні ![]() після обходу довільного замкненого контуру, розміщеного на поверхні
після обходу довільного замкненого контуру, розміщеного на поверхні ![]() , який не перетинає її межу, ми повертаємося з початковим напрямом нормалі
, який не перетинає її межу, ми повертаємося з початковим напрямом нормалі ![]() , то поверхню називають двосторонньою.
, то поверхню називають двосторонньою.
Якщо при обході деякого контуру напрям нормалі змінюється на протилежний, то поверхню називають односторонньою.
Прикладами двосторонніх поверхонь є площина, сфера, довільна замкнена поверхня без самоперетинів, довільна поверхня, задана рівнянням ![]() , де
, де ![]() – функції, неперервні в деякій області
– функції, неперервні в деякій області ![]() площини
площини ![]() .
.
Прикладом односторонньої поверхні є так званий лист Мебіуса (рис. 3).

Рисунок 3 – Лист Мебіуса
Модель цієї поверхні можна отримати, якщо прямокутну полоску паперу![]() , перекрутивши один раз, склеїти так, щоб точка
, перекрутивши один раз, склеїти так, щоб точка ![]() збігалася з
збігалася з ![]() , а точка
, а точка ![]() – з
– з ![]() .
.
Двосторонню поверхню називаютьорієнтовною, а вибір певної її сторониорієнтацією поверхні. Направивши в кожній точці замкненої поверхні нормаль всередину об'єму, обмеженого поверхнею, отримаємо внутрішню сторону поверхні, а направивши нормаль зовні поверхні-зовнішню її сторону. Надалі розглядатимемо двосторонні поверхні. Односторонні поверхні неорієнтовні.
Нехай ![]() – орієнтовна (сторона уже обрана) поверхня, обмежена контуром
– орієнтовна (сторона уже обрана) поверхня, обмежена контуром ![]() , який не має точок самоперетину. Вважатимемо за додатний той напрям обходу контуру
, який не має точок самоперетину. Вважатимемо за додатний той напрям обходу контуру ![]() , при якому спостерігач, розміщений так, що напрям нормалі збігається з напрямом від ніг до голови при русі, залишає поверхню зліва від себе (рис. 4).
, при якому спостерігач, розміщений так, що напрям нормалі збігається з напрямом від ніг до голови при русі, залишає поверхню зліва від себе (рис. 4).
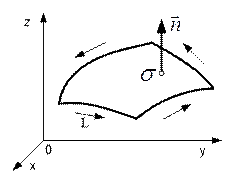
Рисунок 4 – Орієнтовна поверхня ![]()
Протилежний напрям обходу називається від'ємним. Якщо змінити орієнтацію поверхні на протилежну, то додатний і від'ємний напрями обходу контуру ![]() поміняються місцями.
поміняються місцями.
З'ясуємо тепер поняття поверхневого інтеграла другого роду.
Нехай ![]() – гладка поверхня, задана рівнянням
– гладка поверхня, задана рівнянням ![]() і
і ![]() – обмежена функція, визначена в точках поверхні
– обмежена функція, визначена в точках поверхні ![]() . Зорієнтуємо поверхню
. Зорієнтуємо поверхню ![]() . Розіб'ємо її довільно на
. Розіб'ємо її довільно на ![]() частин. Позначимо через
частин. Позначимо через ![]() проекцію
проекцію ![]() -ї частини поверхні
-ї частини поверхні ![]() на площину
на площину ![]() , а через
, а через ![]() – площу
– площу ![]() , взяту із знаком плюс, якщо обрана зовнішня сторона поверхні
, взяту із знаком плюс, якщо обрана зовнішня сторона поверхні ![]() , та із знаком мінус, якщо обрана внутрішня сторона поверхні
, та із знаком мінус, якщо обрана внутрішня сторона поверхні ![]() . Виберемо в кожній частині
. Виберемо в кожній частині ![]() довільну точку
довільну точку ![]() і складемо суму
і складемо суму
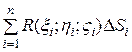 .(6)
.(6)