Реферат: Поверхневі інтеграли

1. Поверхневі інтеграли першого роду

Поверхневі інтеграли першого роду є узагальненням подвійних інтегралів.

Нехай у точках деякої кусково-гладкої поверхні визначена обмежена функція . (Поверхня називається гладкою, якщо в кожній її точці існує дотична площина і при переході від точки до точки положення цієї дотичної площини змінюється неперервно. Поверхня, яка складається із скінченного числа неперервно з’єднаних гладких поверхонь, називається кусково-гладкою.) Розіб'ємо поверхню на довільних частин без спільних внутрішніх точок (рис. 1); нехай – площа, а – діаметр частини поверхні . У кожній частині виберемо довільну точку і складемо суму

.(1)

Рисунок 1– Поверхня

Цю суму називають інтегральною сумою для функції по поверхні .

Якщо при інтегральні суми (1) мають скінченну межу, яка не залежить ні від способу розбиття поверхні , ні від вибору точок , цю границю називають поверхневим інтегралом першого роду від функції по поверхні і позначають .

Таким чином, за означенням

.(2)

У цьому разі функція називається інтегровною по поверхні , а поверхня –областю інтегрування.

Якщо функція неперервна на поверхні , то вона інтегровна по.

Обчислення поверхневого інтеграла першого роду зводиться до обчислення подвійного інтеграла.

Нехай гладка поверхня , задана рівнянням, проектується на площину в область . Припустимо, що функціянеперервна на поверхні , а функції неперервні в області .

Внаслідок розбиття поверхні на частини область розіб'ється на частини , які є відповідними проекціями частин на площину (рис. 2).

Рисунок 2 – Розбиття поверхні на частини

Якщо – площа області , – площа поверхні , то

,

тому інтегральну суму (1) можна записати у вигляді

.(3)

Права частина цієї рівності є інтегральною сумою для функції

,

тому з рівностей (2) і (3) випливає, що

.(4)

Формула (4) виражає поверхневий інтеграл першого роду через подвійний інтеграл по проекції поверхні на площину .

Аналогічно можна отримати формули, що виражають інтеграл по поверхні через подвійні інтеграли по її проекціях на площини та . Якщо поверхня задається рівнянням або , то

,

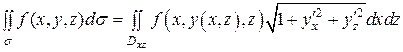
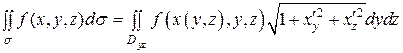--> ЧИТАТЬ ПОЛНОСТЬЮ <--