Реферат: Поверхневі інтеграли

Якщо при інтегральні суми (6) мають скінченну границю, яка не залежить ні від способу розбиття поверхні , ні від вибору точок , то цю границю називають поверхневим інтегралом другого роду і позначають так: . Отже, за означенням

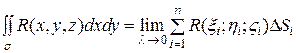.(7)

З означення поверхневого інтеграла другого роду випливає, що при зміні сторони поверхні на протилежну інтеграл змінює знак, бо змінює знак .

Поверхню можна також проектувати на координатні площини та . Тоді матимемо ще два поверхневі інтеграли , де – функції, визначені в точках поверхні .

Оскільки (рис. 5),

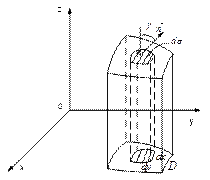
Рисунок 5 – Проекція поверхні на координатну площину

де – елемент площі поверхні – кути між нормаллю до поверхні та осями відповідно, то справедливі такі формули:

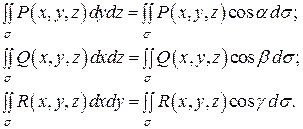
На практиці найпоширенішими є поверхневі інтеграли, які об'єднують усі названі, тобто

.(8)

Якщо, наприклад, вектор є швидкістю рідини, то кількість рідини, яка протікає через поверхню за одиницю часу, називається потоком векторачерез поверхню і знаходиться за формулою:

.

У цьому полягає фізичний зміст поверхневого інтеграла другого роду. Зрозуміло, коли вектор має іншу природу, поверхневий інтеграл має інший фізичний зміст.

Формула (8) виражає загальний поверхневий інтеграл другого роду через поверхневий інтеграл першого роду.

Поверхневі інтеграли другого роду обчислюються за допомогою подвійних інтегралів.

Нехай функція неперервна в усіх точках гладкої поверхні , яка задана рівнянням , де область – проекція поверхні на площину . Виберемо верхню сторону поверхні , де нормаль до поверхні утворює з віссю гострий кут, тоді . Оскільки , то суму (6) можна записати у вигляді

. (9)

У правій частині рівності (9) міститься інтегральна сума для функції . Ця функція неперервна в області , тому інтегрована в ній.

Перейшовши в рівності (9) до границі при , отримаємо формулу

,

яка виражає поверхневий інтеграл другого роду по змінних і через подвійний. Якщо вибрати нижню сторону поверхні (нормаль до поверхні утворює з віссю тупий кут), то одержаний подвійний інтеграл беруть із знаком «мінус», тому

.(10)

Аналогічно

;(11)

.(12)

У формулі (11) гладку поверхню задано рівнянням , а у формулі (12) – рівнянням . Знак «плюс» беремо у цих формулах тоді, коли нормаль до поверхні утворює відповідно з віссю , з віссю гострий кут, а знак «мінус» – коли тупий кут; , – проекції поверхні на площини та відповідно.

Для обчислення загального інтеграла (8) використовують формули (10) – (12), проектуючи поверхню на всі три координатні площини. Таким чином,