Реферат: Поверхневі інтеграли

Перетворимо криволінійний інтеграл, який міститься у лівій частині рівності (17). Оскільки контур лежить на поверхні , то координати його точок задовольняють рівняння , і тому значення функції у точках контуру дорівнюють значенням функції у відповідних точках контуру . Звідси випливає, що

.

Застосовуючи до знайденого інтеграла формулу Гріна, отримаємо

.

Тут підінтегральна функція дорівнює частинній похідній по від складеної функції .

Оскільки – верхня сторона поверхні, тобто ( – гострий кут між нормаллю до поверхні і віссю ), то нормаль має проекції . Але напрямні косинуси нормалі пропорційні відповідним проекціям, тому

,

Тоді

Отже,

.

Аналогічно можна довести, що при відповідних умовах справедливі формули:

;(18)

.(19)

Додаючи почленно рівності (17), (18) і (19), отримуємо формулу

,

яка називається формулою Стокса. За допомогою формули (8), яка пов'язує поверхневі інтеграли першого та другого роду, цю формулу можна записати так:

(20)

Формула Стокса дає змогу обчислювати криволінійні інтеграли по замкнутих контурах за допомогою поверхневих інтегралів.

З формули Стокса випливає, що коли виконуються рівності

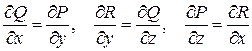,(21)

то криволінійний інтеграл по довільному просторовому замкненому контуру дорівнює нулю:

.(22)

А це означає, що в даному випадку криволінійний інтеграл не залежить від форми контура інтегрування.