Реферат: Предельное равновесие балок и рам

Московский государственный технический

Университет им. Н.Э. Баумана

Калужский филиал

Предельное равновесие балок и рам

Распространенный в практике расчёта машиностроительных конструкций расчёт по допускаемым напряжениям не даёт представления об истинным запасе прочности. Если напряжённое состояние неоднородно, то возникновение пластических деформаций в одной точке ещё не означает наступления предельного состояния для всей конструкции.

Под предельной понимается та нагрузка, при которой исчерпывается способность системы воспринимать возрастающую нагрузку, или такая, при которой возникают столь значительные изменения геометрических размеров системы, что последняя перестаёт удовлетворять своему назначению.

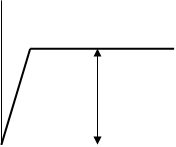
Под термином метод предельного равновесия понимается расчёт систем в предположении, что материал их имеет диаграмму '' s-e '' с неограниченной площадкой текучести (Рис.1). Начальный участок диаграммы соответствует упругой работе материала с модулем упругости Е и верхней границей, равной s_y . Горизонтальный участок – идеальной пластичности материала (деформации неограниченно растут при стабильном ном напряжении). Такая диаграмма называется обычно диаграммой идеально упругопластического тела или диаграммой Прандтля .

s

s_y

0 e

Рис. 1

1. Предельный момент для сечения балки

При значениях изгибающего момента М >s_т W_x поперечное сечение балки переходит в упругопластическое состояние. По мере роста деформаций, упругое ядро сечения сокращается и в пределе эпюра нормальных напряжений приобретает вид двух прямоугольников ( Рис. 2 ). Это состояние сечения и будем считать предельным.

Зависимость между кривизной оси балки и изгибающим моментом будет иметь вид, изображённый на Рис. 3. Учитывая, что в расчет уже внесена погрешность, обусловленная принятием диаграммы Прандтля, аппроксимируем зависимость ''кривизна – момент'' двумя отрезками прямых.

Ys_y М

А^-

x₀ s_y W_x м_u

Истинная зависимость

А⁺ 1/r

0 _{КРИВИЗНА БАЛКИ}

s_y

Рис. 2 Рис. 3

Обратим внимание на то, что зависимость между М и 1/r подобна диаграмме Прандтля. Предельное состояние сечения считается достигнутым сразу после окончания упругой стадии работы сечения, которая несколько продлевается за счёт упругой стадии. Значение момента, соответствующее предельному состоянию, называется предельным моментом. Предельному моменту соответствует неопределённое значение кривизны от М_пр / ЕI_x до ¥. Эта условная стадия работы сечения называется пластическим шарниром.

Предельный момент можно вычислить, как момент внутренних сил сечения относительно нейтральной оси в предельном состоянии x₀ (Рис.2). Полагая пределы текучести при растяжении и сжатии одинаковыми и равными s_y , получим:

М_u = òs_y ydA + òs_y ydA = s_y ( êS_xo ⁺ ê + êS_xo ^- ê) = s_y W_пл ;

A⁺ A^-

W_пл = çS_xo ⁺ ç + çS_xo ^- ç- пластический момент сопротивления;

S_xo ⁺ и S_xo ^- -cтатические моменты, соответственно, растянутой и сжатой зоны сечения (Рис. 2), взятые относительно оси x₀ . Положение оси x₀ найдётся из условия, что она делит сечение на две равновеликие по площади части: А⁺ = А^- .

Итак! Сечение, перешедшее в предельное состояние, ведёт себя подобно шарниру. Пластический шарнир имеет следующие отличия:

1) в нём действует изгибающий момент, равный M_u ;

2) он односторонний;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--