Реферат: Применение новейших экономико-математических методов для решения задач

Вышеизложенный способ получения решения уравнения может быть легко распространен для случая решения системы двух уравнений с двумя неизвестными, если система имеет следующий вид:

Y=Ф(x )

Y=Ψ(x ) (3)

Преобразуем систему (3) в одно уравнение вида (4):

Ф(x )- Ψ(x )=0 (4)

Полученное уравнение уже можно решить с помощью Подбор параметра… так как это было описано выше.

Рассмотрим нахождение равновесной цены и объема продаж для рынка некоторого товара.

Пусть функция спроса на товар имеет вид Q_d =80e ^-0.05p -20 , 0≤ p ≤30 , а функция предложения Q_s =12p-3e^0.02p , 0≤p≤30 .

Найти равновесные цену и объем, построить графики спроса и предложения. Имеющуюся систему уравнений

Q_d =80e^-0.05p -20

Q_s =12p-3e^0.02p

преобразуем в одно уравнение вида 80e^-0.05p -20 - 12p+3e^0.02p =0 .

Подбор параметра… описанным выше, находим равновесную цену, она равна 4,049213, подставив это значение в одно из уравнений системы. Получим и значение равновесного объема - 45,33749 . Для построения графика, иллюстрирующего ситуацию равновесия спроса и предложения на рынке, воспользуемся знанием равновесной цены и возьмем значения в некоторой окрестности от нее. Получим следующую иллюстрацию решения задачи о равновесии на рынке (рис.6.).

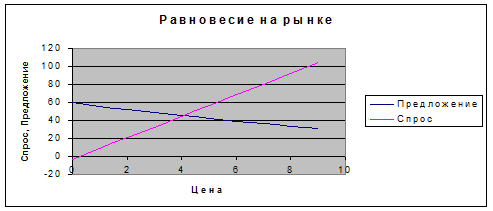рис.6.

Глава №2 Матричная алгебра

Матричная алгебра тесно связана с линейными функциями и с линейными ограничениями, в связи, с чем находит себе применение в различных экономических задачах:

· в эконометрике, для оценки параметров множественных линейных регрессий;

· при решении задач линейного программирования;

· при макроэкономическом программировании и т.д.

Особое отношение к матричной алгебре в экономике появилось после создания моделей типа «Затраты-Выпуск», где с помощью матриц технологических коэффициентов объясняется уровень производства в каждой отрасли через связь с соответствующими уровнями во всех прочих отраслях.

Электронная таблица EXCEL имеет ряд встроенных функций для работы с матрицами:

ТРАНСП – транспонирование исходной матрицы;

МОПРЕД – вычисление определителя квадратной матрицы;

МОБР – вычисление матрицы обратной к данной;

МУМНОЖ – нахождение матрицы, являющейся произведением двух матриц.

Кроме того, возможно выполнение операций поэлементного сложения (вычитания) двух матриц и умножения (деления) матрицы на число.

На примере проиллюстрируем некоторые из этих функций. Найдем сумму двух матриц А(5*4) и В(5*4) и транспонируем матрицу-результат.

2.1 Сложение матриц

Задание #3

Для сложения двух матриц одинаковой размерности следует выполнить следующую последовательность действий:

1. Задать две исходных матрицы.

2. Отметить место для матрицы-результата.