Реферат: Применение новейших экономико-математических методов для решения задач
3.
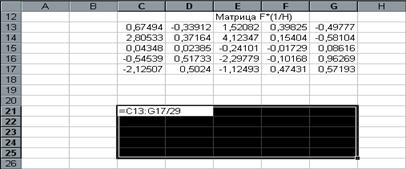 |
? ?????????? ??? ????????? ????? ??????????? ??????? ???????? ???????????? ???, ??? ???????? ?? ???.15.
рис.15.
4.
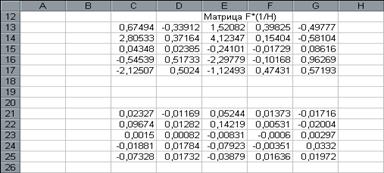 |
????????? ?????????? ?????? ???????? ?????? Shift /Ctrl /Enter (???.16.).
рис.16.
2.6 Сложение матриц
Для сложения двух матриц одинаковой размерности следует выполнить следующую последовательность действий:
1.Задать две исходные матрицы.
2.Отметить место для матрицы-результата.
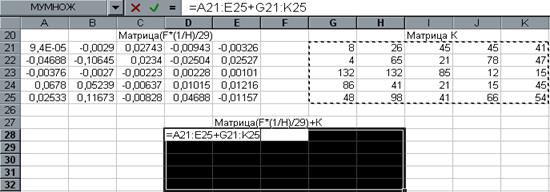 |
3.? ?????????? ??? ????????? ????? ??????????? ??????? ???????? ????? ???, ??? ???????? ?? ???.17.
рис.17.
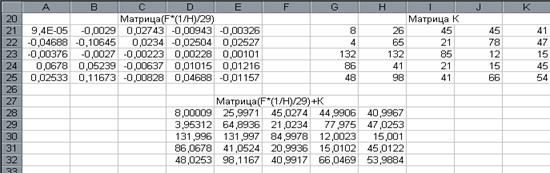 |
4.????????? ?????????? ?????? ???????? ?????? Shift /Ctrl /Enter (???.18.).
рис.18.
2.7 Вычисление определителя матрицы
Для вычисления определителя матрицы сформируем лист электронной таблицы:
1.Определим исходную матрицу.
2.Определим место под результат.
3.Обратимся к мастеру функций, найдем функцию МОПРЕД , выполним постановку задачи (рис.19.).
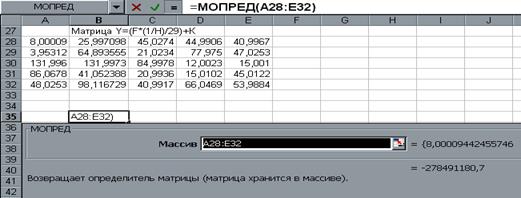 |
рис.19.
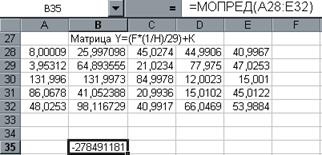 |
4.??????? ?? ?????? ОК , ??????? ???????? ???????????? (???.20.).
рис.20.
2.8 Системы линейных алгебраических уравнений
Задание #5
Решение систем линейных алгебраических уравнений всегда занимало математиков и для их решения было разработано немало численных методов, подразделяющихся на прямые и итерационные.
В EXCEL задача получения решения СЛАУ решается с помощью вышеописанных матричных функций, для чего исходную систему надо представить в виде матричного уравнения.
Рассмотрим последовательность действий для получения решения СЛАУ на конкретном примере.
![]() -12X1 +12X2 +23X3 +6X4 =120
-12X1 +12X2 +23X3 +6X4 =120
-3X1 +0.3X2 -3X3 +X4 =-25
-67X1 -3X2 -51X3 -73X4 =536 (5)
-91X1 -6X2 +4X3 -13X4 =-316
Для того, чтобы система (5) имела единственное решение необходимо и достаточно, чтобы определитель системы, составленный из коэффициентов при переменных Х1 , Х2 , Х3 , Х4 , не был равен нулю.
Рассчитаем определитель системы, пользуясь функцией МОПРЕД (рис.21.). Рассчитанное значение определителя системы равно –12. Оно не равно нулю и, следовательно, можно продолжать процесс поиска решения.
Из линейной алгебры известна матричная запись системы уравнений и матричное представление решения. Перепишем систему (5) в виде
АХ=В, где![]()
![]()
-12 12 23 6
|
-67 -3 -51 -73
-91 -6 4 -13
![]()
![]()
Х1
|