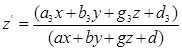Реферат: Проективная геометрия

s^/ _k x^/ _{2 k} =c₂₁ x_{1 k} +c₂₂ x_{2 k} +c₂₃ x_{3 k} +c₂₄ x_{4 k}

(2)

s^/ _k x^/ _{3 k} =c₃₁ x_{1 k} +c₃₂ x_{2 k} +c₃₃ x_{3 k} +c₃₄ x_{4 k}

s^/ _k x^/ _{4 k} =c₄₁ x_{1 k} +c₄₂ x_{2 k} +c₄₃ x_{3 k} +c₄₄ x_{4 k}

с постоянными коэффициентами с_{i k} и при этом определитель матрицы такого преобразования D=с=(с_{i k} ) №0.

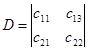3) Аналогичные определения существуют при проективном отображении прямой a на прямую a^/ . Если М^/ - точка на прямой а^/ с однородными координатами х^/ ₁ , x^/ ₂ ,и точка М - на прямой а с однородными координатами x₁ , x₂ ,то проективное преобразование М^/ = f (M) однозначно определяется из соотношений:

s^/ x^/ ₁ = c₁₁ x₁ +c₁₂ x₂

s^/ x^/ ₂ = c₂₁ x₁ +c₂₂ x₂ и

Часто бывает удобным использовать проективные преобразования в неоднородных координатах.

Для прямой : Если х₁ , х₂ - однородные координаты точки М на прямой ,то х=х₁ / x₂ - число, являющееся неоднородной координатой точки М на этой прямой . Пусть задано проективное преобразование прямой а на прямую а^/ . Значит, существуют соотношения :

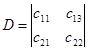
sx^/ ₁ = c₁₁ x₁ +c₁₂

sx^/ ₂ =c₂₁ x₁ +c₂₂ x₂

Разделим почленно первое равенство на второе :

sx^/ ₁ /sx^/ ₂ =(c₁₁ x₁ +c₁₂ x₂ ) / (c₂₁ x₁ +c₂₂ x₂ ) , учитывая , что x^/ =x^/ ₁ / x^/ ₂ , и x=x₁ / x₂ .

Преобразуем

x^/ =(c₁₁ x+c₁₂ )/ (c₂₁ x+c₂₂ ) , введя новые обозначения : a=c₁₁ , b=c₁₂ , g=c₂₁ , d=c₂₂

x^/ =(ax+b) / (gx+d) - т.е. в неоднородных координатах проективное преобразование выражается дробно - линейной функцией. ad -bg №0

Для плоскости : Однородные координаты точки М - х₁ , х₂ , х₃ , неоднородные : x=x₁ / x₃ ,y=x₂ / x₃ .

Формулы проективного преобразования в неоднородных координатах :

x^/ =(a₁ x+b₁ y+c₁ ) / (ax+by+ g) , a₁ b₁ c₁ y^/ =(a₂ x+b₂ y+c₂ ) / (ax+ by+ g) где

В трехмерном пространстве :

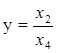
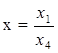
Однородные координаты (x₁ , x₂ , x₃ , x_{4 )} ) _.

Неоднородные координаты