Реферат: Пространство и время в физике. Системы отсчета. Принципы относительности. Преобразования Галилея

1. Пространство и время в физике. Системы отсчета. Принципы относительности. Преобразования Галилея и Лоренца и их следствия.

Нерелятивистская или иначе классическая концепция восходит к Ньютону. Согласно ей пространство есть абсолютное вместилище для тел. Это трех мерное Евклидово пространство. Оно – данность, не от чего не зависящая, не от тел, не от времени. Классическое пространство – бестелесный образ абсолютно твердого тела.

Время в нерелятивистской концепции – абсолютная длительность. Время всеобщее, глобальное. Оно течет одинаково во всех пространственных точках. Время так же как и пространство абсолютная данность, не зависящее не от тел, не от пространства

В релятивистской концепции пространство и время изначально взаимосвязаны друг с другом – они есть составляющие единого, цельного объекта – пространство-времени. О них нельзя говорить порознь. Кроме того, здесь нет общего глобального времени, а есть множество собственных (инвариантных) времен. Пространство-время представляет собой четырехмерное пространство событий с псевдоевклидовой геометрией.

Система отсчета – пространственно временная конструкция, предназначенная для определения временной и пространственной координат локальных, точечных событий.

Различают инорциальные и неинорциальные с.о. По определению и.с.о. есть такая с.о. относительно которой свободная частица либо покоится, либо движется равномерно и прямолинейно. Другое определение: и.с.о. такая с.о. в которой пространство однородно и изотропно, а время однородно.

Соответственно: н.с.о. такая с.о. относительно которой свободные частицы движутся с ускорением. В такой с.о. пространство и время неоднородно.

Принцип относительности – принцип симметрии или эквивалентности всех и.с.о. Классический п.о. утверждает эквивалентность всех и.с.о. относительно только механический явлений. Релятевисский п.о. гласит, что все и.с.о.эквивалентны относительно любых физический явлений.

Классические представления о пространстве и времени выражаются преобразованиями Галилея: (картинка).

А – событие, локальный физический акт, совершаемый в определенной точке пространства, в определенный момент времени.

А имеет 2 характеристики: физическое содержание и пространственно – временную характеристику.

Как связаны координаты А в системе k и k^/ ?

Исходя из п.о. искомая связь должна быть линейной, только в этом случае система будет двигаться равномерно и прямолинейно по отношению к k и k^/ .

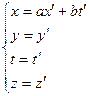
- согласно абсолютности времени.

Найдем а и b. Рассмотрим А(0, t^/ ) и А(х = vt,t) подставим в систему.

, . Получим .

Рассмотрим В(0,t) , В(-vt^/ ,t^/ ) подставим в предыдущее уравнение.

а = 1.

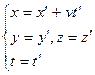- преобразования Галилея .

следствия: - абсолютной одновременности.

Расстояния инвариантны, абсолютны.

Релятивистские представления о пространстве и времени выражаются преобразованиями Лоренца: (картинка).

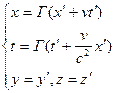- преобразования Лоренца. Где .

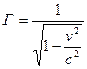В области малых скоростей они принимают форму преобразований Галилея.

Следствия: , то есть события одновременные в одной и.с.о. не одновременные в другой. Одновременность относительная.

До световая скорость будет в любой с.о. до световой.

2. Схемы классической механики. Динамические уравнения. Законы сохранения.

Теоретически схема Ньютона есть схема векторно-силовой механики. Основная величина вектор силы . Состояние частицы определяется тремя этими параметрами. Динамическое уравнение: (второй закон Ньютона).

В случае механической системы частиц состояние определяется набором координат и скоростей. И динамическое уравнение будет: (1) ., где - результирующая всех внутренних сил, действующих на итую частицу.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--