Реферат: Пространство и время в физике. Системы отсчета. Принципы относительности. Преобразования Галилея

В случае замкнутой системы: , то есть ее импульс есть величина постоянная по времени. , то ее суммарный момент импульса, является интегралом движения, величиной не изменяющийся при движении механической системы.

Из (2) следует : (3) – законы сохранения импульса и момента импульса.

Если действующие внутренние силы консервативны, то мы определим потенциальную энергию: (это такая энергия, за счет убыли которой совершается работа). Используя здесь закон изменения кинетической энергии получим: . (4). – закон сохранения энергии.

Теоретически схемы классической механики Лагранжа и Гамильтона можно назвать скалярно-энергетическими.

В механике Лагранжа состояние системы определяется следующим набором - число степеней свободы. - обобщенные координаты, это любые параметры полностью и однозначно определяющие положение частиц системы в пространстве. - обобщенные скорости, производные от координат .

Динамическое уравнение консервативной системы – уравнение Лагранжа.

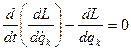(5). - функция Лагранжа, функция состояния.

Для консервативных систем (кинетич. – потенц.).

Уравнения Лагранжа – система s – штук дифференциальных уравнений второго порядка. Любые динамические уравнения нужны для того чтобы решить основную задачу механики: найти интегральный закон движения системы.

С функцией Лагранжа связаны законы сохранения:

1) если явно не зависит от времени, то имеет место закон сохранения энергии: .

2) если функция Лагранжа явно не зависит от какой то координаты , то обобщенный импульс - закон сохранения импульса.

Теоретическая схема механики Гамильтона:

Состояние системы определяется набором всех обобщенных координат, обобщенных импульсов взятых в соответствующий момент времени. .

Основная функция состояния - функция Гамильтона. .

Динамическое уравнение : . Система 2s дифференциальных уравнений первого порядка.

Законы сохранения:

1) если явно не зависит от времени, то полная энергия сохраняется. .

2) Если Н не зависит от , то соответствующий обобщенный импульс - закон сохранения импульса.

3. Задача двух тел в классической механике. Движение частицы в центрально – симметричном поле. Закон всемирного тяготения.

Задача двух тел: в лабораторной с.о. задана замкнутая система двух частиц, массами m₁ и m₂ . Известна энергия их взаимодействия - потенциальная энергия от расстояния . Требуется определить закон движения каждой частицы.

Задача решается в центральной с.о. – с.о. центра масс системы, так как нужно исключить движение системы как целого. С.о. связанная с центром масс – система в которой полный импульс равен 0 .

Запишем дифференциальные уравнения движения частицы: 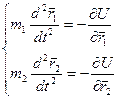(1) справа от = сила, так как

. .

Тогда получаем: . После подстановки этого в (1) они становятся одинаковыми: . Где - приведенная масса двух частиц.

Т.о. задача двух тел сводится к задаче о движении одной фиктивной частицы массой , в центрально – симметричном поле.

Рассмотрим особенности движения частицы в центрально – симметричном силовом поле. Пусть точка О – центр поля. (картинка: вектор от точки О к точке m)

, след. сила направлена по радиус-вектору.

Найдем момент импульса частицы относительно центра поля.