Реферат: Пространство и время в физике. Системы отсчета. Принципы относительности. Преобразования Галилея

Если , то m = 0. Из (1) следует существование безмассовых частиц. Примером такой частицы является фотон.

Полная энергия , - собственная энергия частицы, .

Динамическое уравнение: .

В случае системы частиц масса системы как целого определяется

.

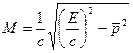
, где - собственная кинетическая энергия в ценральной с.о.

т.о. - не аддитивность релятивистских масс. В случае локальной системы взаимодействующих частиц: , то есть < .

6. Электромагнитное взаимодействие. Закон сохранения эл.заряда. Электромагнитное поле. Сила Лоренца. Относительный характер эл.магнитной компоненты электромагнитного поля.

Электромагнитное взаимодействие – взаимодействие заряженных тел, посредством электромагнитного поля. Заряженное тело – тело, обладающее зарядом. Заряд есть свойство заряженных тел. Оно проявляется в том, что:

1) заряженное тело является источником электромагнитного поля,

2) заряженное тело реагирует на силовое действие электромагнитного поля.

Величина заряда определяется в физических измерениях, по тем или иным проявлениям электромагнитного взаимодействия. Например посредством закона Кулона.

Заряд – величина скалярная и выражается действительным числом: <0, =0, >0. кроме того , относительно преобразований Лоренца. Заряд – величина аддитивная: заряд любой системы заряженных тел или частиц = алгебраической сумме зарядов отдельных тел. Заряд кратен элементарному заряду: Кл. – это электрон, а + - позитрон.

То есть заряд по природе дискретен. Закон сохранения заряда относится к фундаментальным законам физики. Он гласит: в изолированной системе электрический заряд сохраняется, то есть (1).

Если заряд есть свойство заряженных тел и частиц, то электромагнитное поле – вид материи (отличный в макромире от вещества). Его основное свойство – нелокализуемость. Кроме того, оно обладает проницаемостью. В общем случае электромагнитное поле переменное, оно стремиться рассеяться в пространстве.

Электромагнитное поле как физический объект характеризуется энергией, импульсом и моментом импульса. В модели Максвелла эти величины не используются в качестве исходных характеристик электромагнитного поля (так как они не отражают его специфики). К таким первичным характеристикам относятся электрический Е и магнитный В векторы. Посредством их выражается силовое действие электромагнитного поля, на внесенный в него электрический заряд.

Величины Е и В определяются равенствами: (2)

Где - силы действия электромагнитного поля.

В общем случае на точечный заряд в электромагнитном поле действует сила Лоренца: (складывается из электрических и магнитных сил).

Электромагнитное поле – целостный объект. Его разделение на эл. и маг. составляющие – относительно, зависит от выбора ИСО.

Электромагнитное поле предельно релятивистский объект. Как целостный объект оно характеризуется релятивистсими инвариантами ( величины сохраняющиеся относительно преобразований Лоренца):

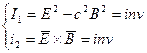(4). Это значит, что если электромагнитное поле рассматривать относительно систем k и k^/ , то

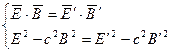(5) здесь имеет место законы преобразования декартовых компонент векторов Е и В:

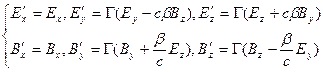(6). Где , .

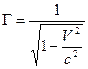Из (6) следует, если , то .

7. Взаимод.непод.зарядов(закон Кулона), взаимод.эл.токов (закон Ампера), электромагнит.индукции (закон Фарадея). Уравнение Максвелла .

2 неподвижных точечных заряда взаимодействуют с силами, прямопропорциональными произведению модулей зарядов и обратнопропорциональными квадрату расстояния между ними. 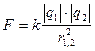- это в вакууме. k - постоянная Кулона . - электрическая постоянная, входящая в число фундаментальных постоянных.

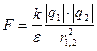- в веществе. - диэлектрическая постоянная среды, показывающая во сколько раз взаимодействие зарядов в среде слабее, чем в вакууме.

Закон Кулона в векторной форм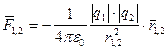е: . Где - сила, действующая на 1 заряд со стороны 2. - радиус-вектор от 1 ко 2.