Реферат: Расчет привода швейной иглы
м/с2
Модуль углового ускорения шатуна 2 можно вывести из формулы (1.19):
1/с2
Перенесем вектор ускорения 
с плана ускорений в точку С3 плана механизма, и увидим, что угловое ускорение e2 направлено против часовой стрелки.
1.6. Расчет уравновешивающего момента.
При расчете мощности двигателя необходимо знать величину уравновешивающего (движущего) момента, приложенного к главному валу для обеспечения заданного закона его движения (w1 =const ). Решить поставленную задачу можно методом профессора Н.Е. Жуковского.
Согласно теореме профессора Н.Е. Жуковского, если силу, приложенную к какой-либо точке звена механизма, перенести параллельно самой себе в одноименную точку повернутого на 90о плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности.
На основании общего уравнения динамики:
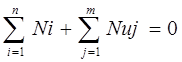(1.24)
где Ni – мощность i-той внешней силы;
Nuj – мощность j-той силы инерции.
В соответствии с теоремой профессора Н.Е. Жуковского уравнение (1.24) равносильно уравнению моментов сил относительно полюса повернутого плана скоростей:
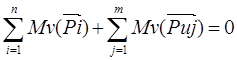(1.25)
По условию нам дано, что m3 =0,035 кг (масса поступательно движущихся частей кривошипно-ползунного механизма), масса кривошипа (исходя из того, что в 1 мм содержится 2 грамма) m1 =0,03 кг, масса шатуна (исходя из того, что в 1 мм содержится 2,5 грамма) m2 =0,0975 кг, сила полного сопротивления 
=5,5 Н .
Момент инерции шатуна относительно центра масс S2 можно определить по зависимости:
(1.26)
Вычерчиваем план механизма в первом положении без изменения масштаба, т.е. kl =0,00015 м/мм .
Определяем силовые факторы, приложенные к звеньям.
Силы тяжести:
G1 =m1 g=0 , 29 Н
G2 =m2 g=0,96 H
G3 =m3 g=0.34 H
Все звенья движутся с ускорением, следовательно, к ним приложены силы инерции:
(1.27)
где 
- вектор полного ускорения центра масс.
Знак минус в уравнении (1.27) означает, что сила инерции и ускорение центра масс направлены в разные стороны.
Модули сил инерции:
Н
Н
Н
Момент инерционных сил, приложенных к шатуну 2 :
(1.28)
Знак минус показывает, что направления момента инерционных сил и углового ускорения разные.
Момент инерции шатуна, согласно уравнению (1.26): 
Момент инерционных сил, согласно уравнению (1.28): 
. Направлен этот момент по часовой стрелке.
Момент инерционных сил и уравновешивающий момент заменим парами сил.