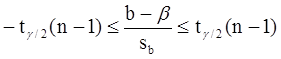Реферат: Регрессионный анализ. Парная регрессия

y_i ¹a + bx_i + e_i

Вопрос: почему бы нам не взять g поменьше? Чем меньше g, тем больше соответствующее табличное значение F-статистики, т. е., тем меньше шансов, что появятся основания отвергнуть гипотезу Н₀ .

Ошибки первого и второго рода

Ошибка первого рода: отвергается Н₀ , которая на самом деле верна.

Ошибка второго рода: принимается H0, которая на самом деле не верна.

Очевидно, чем меньше g, тем меньше наши шансы отвергнуть гипотезу Н₀ , т. е., совершить ошибку первого рода. Соответственно, шансы совершить ошибку второго рода увеличиваются.

4. Характеристика оценок коэффициентов уравнения регрессии

1) математическое ожидание

Теорема: М(а) = a, M(b) = b - несмещенность оценок

Это означает, что при увеличении количества наблюдений значения МНК-оценок a и b будут приближаться к истинным значениям a и b;

2) дисперсия

Теорема:

;

Благодаря этой теореме, мы можем получить представление о том, как далеко, в среднем, наши оценки a и b находятся от истинных значений a и b.

Необходимо иметь в виду, что дисперсии характеризуют не отклонения, а «отклонения в квадрате». Чтобы перейти к сопоставимым значениям, рассчитаем стандартные отклонения a и b:

;

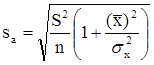Будем называть эти величины стандартными ошибками a и b соответственно.

5. Построение доверительных интервалов

Пусть мы имеем оценку а. Реальное значение коэффициента уравнения регрессии a лежит где-то рядом, но где точно, мы узнать не можем. Однако, мы можем построить интервал, в который это реальное значение попадет с некоторой вероятностью. Доказано, что:

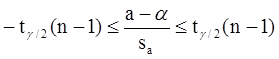
с вероятностью Р = 1 - g

где t_{g /2} (n-1) - g/2-процентная точка распределения Стьюдента с (n-1) степенями свободы – определяется из специальных таблиц.

При этом уровень значимостиg устанавливается произвольно.

Неравенство можно преобразовать следующим образом:

,

или, что то же самое:

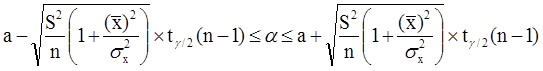
Аналогично, с вероятностью Р = 1 - g: