Реферат: Регрессионный анализ. Парная регрессия

,

или:

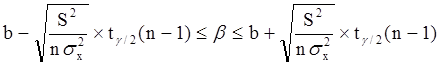
Уровень значимости g - это вероятность того, что на самом деле истинные значения a и b лежат за пределами построенных доверительных интервалов. Чем меньше его значение, тем больше величина t_{g /2} (n-1), соответственно, тем шире будет доверительный интервал.

6. Проверка статистической значимости коэффициентов регрессии

Мы получили МНК-оценки коэффициентов, рассчитали для них доверительные интервалы. Однако мы не можем судить, не слишком ли широки эти интервалы, можно ли вообще говорить о значимости коэффициентов регрессии.

Гипотеза Н₀ : предположим, что a=0, т. е. на самом деле независимой постоянной составляющей в отклике нет (альтернатива – гипотеза Н₁ : a¹ 0).

Для проверки этой гипотезы, с заданным уровнем значимости g, рассчитывается t-статистика, для парной регрессии:

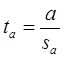
Значение t-статистики сравнивается с табличным значением t_{g /2} (n-1) - g/2-процентной точка распределения Стьюдента с (n-1) степенями свободы.

Если |t| < t_{g /2} (n-1) – гипотеза Н₀ не отвергается (обратить внимание: не «верна», а «не отвергается»), т. е. мы считаем, что с вероятностью 1-g можно утверждать, что a = 0.

В противном случае гипотеза Н₀ отвергается, принимается гипотеза Н₁ .

Аналогично для коэффициента b формулируем гипотезу Н₀ : b = 0, т. е. переменная, выбранная нами в качестве фактора, на самом деле никакого влияния на отклик не оказывае.

Для проверки этой гипотезы, с заданным уровнем значимости g, рассчитывается t-статистика:

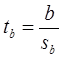
и сравнивается с табличным значением t_{g /2} (n-1).

Если |t| < t_{g /2} (n-1) – гипотеза Н₀ не отвергается, т. е. мы считаем, что с вероятностью 1-g можно утверждать, что b = 0.

В противном случае гипотеза Н₀ отвергается, принимается гипотеза Н₁ .

7. Автокорреляция остатков.

1. Примеры автокорреляции.

Возможные причины:

1) неверно выбрана функция регрессии;

2) имеется неучтенная объясняющая переменная (переменные)

2. Статистика Дарбина-Уотсона

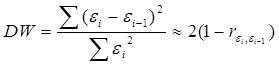
Очевидно:

0 £ DW £ 4

Если DW близко к нулю, это позволяет предполагать наличие положительной автокорреляции, если близко к 4 – отрицательной.

Распределение DW зависит от наблюденных значений, поэтому получить однозначный критерий, при выполнении которого DW считается «хорошим», а при невыполнении - «плохим», нельзя. Однако, для различных величин n и g найдены верхние и нижние границы, DW_L и DW_U , которые в ряде случаев позволяют с уверенностью судить о наличии (отсутствии) автокорреляции в модели. Правило: