Реферат: Решение финансовых и оптимизационных задач в Microsoft Excel
Ставка – ставка дисконтирования за один период.
Значение1, значение2 ,… – от 1 до 29 аргументов, представляющих расходы и доходы.
- Значение1, значение2 , … должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
- ЧПС использует порядок аргументов значение1, значение2 , … для определения порядка поступлений и платежей. Необходимо, чтобы платежи и поступления введены в правильном порядке.
- Аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел, учитываются; аргументы, которые являются значениями ошибки или текстами, которые не могут быть преобразованы в числа, игнорируются.
- Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст или значения ошибок в массиве или ссылке игнорируются.
- Считается, что инвестиция, значение которой вычисляет функция ЧПС , начинается за один период до даты денежного взноса значение1 и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС , но не включать в список аргументов.
- ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от денежных взносов переменной величины в функции ЧПС , денежные взносы в функции ПС должны быть постоянны на весь период инвестиции.
Для приведенного на рис 3.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 3.2.
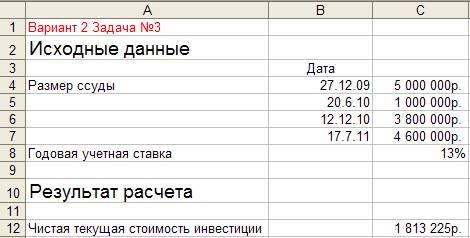
Рисунок 3.1
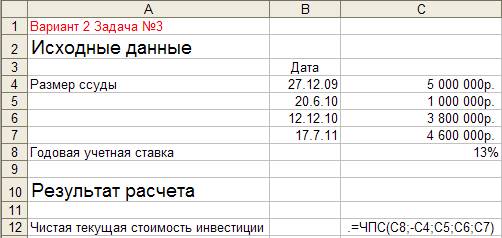
Рисунок 3.2
Задача № 4 (Вариант 2 Задача № 4)
Для приведенного на рис 4.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 4.2.
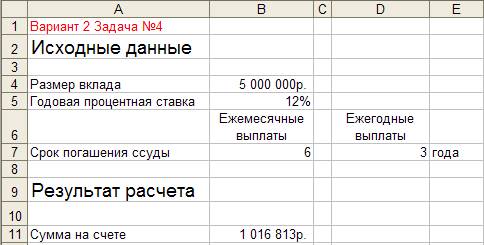
Рисунок 4.1
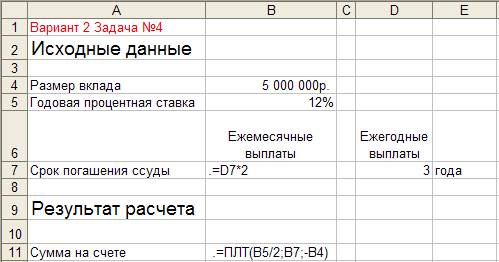
Рисунок 4.2
Задача № 5 (Вариант 2 Задача № 5)
Для приведенного на рис 5.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 5.2.
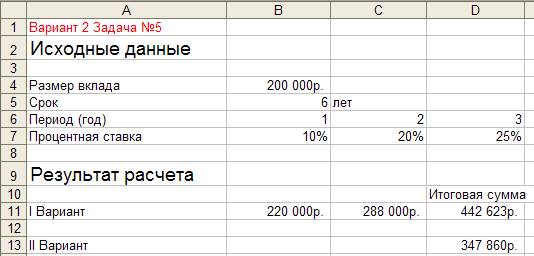
Рисунок 5.1
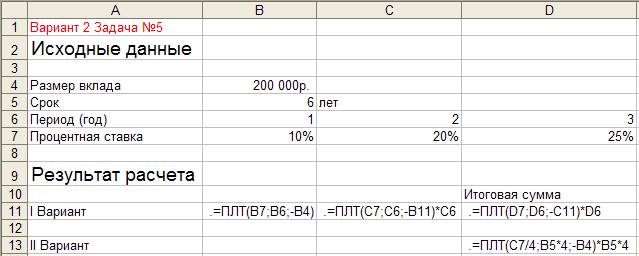
Рисунок 5.2
Из результатов расчета видно, что для фирмы предпочтительнее приобрести облигацию.
II Решение оптимизационных задач линейного программирования
Линейное программирование (ЛП) – это метод оптимизации моделей, в которых целевые функции и ограничения строго линейны. ЛП успешно применяется в военной области, индустрии, сельском хозяйстве, транспортной отрасли, экономике, системе здравоохранения и даже в социальных науках. Широкое использование этого метода также подкрепляется высокоэффективными компьютерными алгоритмами, реализующими данный метод. На алгоритмах линейного программирования (учитывая их компьютерную эффективность) базируются оптимизационные алгоритмы для других, более сложных типов моделей и задач исследования операций, включая целочисленное, нелинейное и стохастическое программирование.
Задача (модель) ЛП, как и любая задача исследования операций, включает три основных элемента.
1. Переменные, которые следует определить.
2. Целевая функция, подлежащая оптимизации.
3. Ограничения, которым должны удовлетворять переменные.
Определение переменных – первый шаг в создании модели. После определения переменных построение ограничений и целевой функции обычно не вызывает трудностей.
Задача № 6 (Вариант 6 Задача № 1)
В данной задаче необходимо спланировать объем производства так, чтобы максимизировать прибыль. Обозначим через ![]() ,
, ![]() ,
, ![]() – объемы производства трельяжа, трюмо и тумбочки под телевизор соответственно. Суммарная прибыль от производства равна:
– объемы производства трельяжа, трюмо и тумбочки под телевизор соответственно. Суммарная прибыль от производства равна:
![]() .
.
Целью комбината является определение среди всех допустимых значений ![]() ,
, ![]() ,
, ![]() таких, которые максимизируют суммарную прибыль, т. е. целевую функцию
таких, которые максимизируют суммарную прибыль, т. е. целевую функцию ![]() . Перейдем к ограничениям, которые налагаются на
. Перейдем к ограничениям, которые налагаются на ![]() ,
, ![]() ,
, ![]() . Объем производства мебели не может быть отрицательным, следовательно:
. Объем производства мебели не может быть отрицательным, следовательно:
![]() .
.
Расход древесно-стружечных плит для производства всех видов мебели не может превосходить максимально возможный запас, следовательно:
![]() ,
,
![]() ,
,
![]() .
.
Кроме того, общая трудоемкость для производства всех видов мебели не должна превосходить плановый фонд рабочего времени, следовательно:
![]()
Таким образом, математическая модель данной задачи имеет следующий вид:
максимизировать
![]()
при следующих ограничениях: