Реферат: Решение систем дифференциальных уравнений

Реферат

на т ем у :

"Решение систем дифференциальных уравнений"

1. Дифференциальная линейная алгебра

С собственными значениями и векторами матрицы приходится иметь дело в задачах, связанных с решением систем линейных дифференциальных уравнений и исследованием устойчивости этих решений. Дифференциальная векторно-матричная алгебра включает в себя операции интегрирования и дифференцирования, которые во множестве случаев в своей нотации напоминают соответствующие операции обычного дифференциального исчисления. Производная по скалярной переменной и интеграл от вектора и матрицы в заданных пределах изменения скалярной переменной определены так:

Производные от векторных и векторно-матричных выражений определяются следующими правилами:

,

,

,

,

.

2 . Векторное решение однородного уравнения

Пусть система линейных однородных дифференциальных уравнений задана в векторной форме:

Если уравнение записано в форме однородного дифференциального уравнения n -го порядка и его характеристический многочлен имеет различные корни, то общее решение представляется суммой n частных решений с экспоненциальными базовыми функциями:

,

где – константы, определяемые начальными условиями.

Можно предположить, что векторное уравнение, представляющее общее решение, имеет аналогичную форму

.

Для выяснения вопроса, что есть в таком представлении и , подставим частное решение в уравнение:

Отсюда видно, что будет частным решением, если будут собственным значением и собственным вектором матрицы A.

Таким образом, если матрица A имеет собственные значения и векторы , k=1,2,…, n, то общее решение однородного векторного уравнения после ряда эквивалентных преобразований предстанет в следующем виде:

.

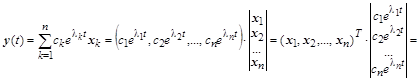
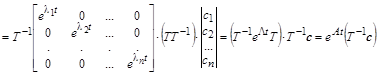Используя значение решения при t= 0, находим . Таким образом, общее решение однородного векторного уравнения имеет следующий вид: .

Матричная экспонента выражается через проекторы и собственные значения матрицы по формулам спектрального разложения:

.

После подстановки X в решение вместо экспоненты получим:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--