Реферат: Решение систем дифференциальных уравнений

Использование формулы трапеций приводит после соответствующих преобразований к следующей рекуррентной формуле:

Если использовать формулу Симпсона, то рекуррентная формула для расчета переходного процесса от точки к точке будет такой:

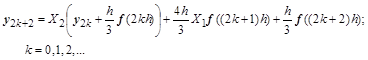
В приведенных рекуррентных формулах матричные экспоненты имеют следующий вид:

.

4. Примеры численного решения векторно-матричных уравнений

В качестве примера построим переходный процесс для системы уравнений:

.

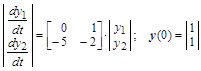Эта система может быть представлена дифференциальным уравнением второго порядка относительно переменной :

,

или относительно переменной :

.

Характеристическое уравнение имеет два комплексных корня: . Общее решение этих уравнений будет:

,

где – постоянные, которые вычисляются по заданным начальным условиям путем решения системы уравнений:

Несложные преобразования приводят к следующим точным решениям этого уравнения для двух различных наборов начальных условий:

Получим такое же аналитическое решение векторного переходного процесса в форме экспоненциальной функции, используя спектральное разложение матрицы по собственным значениям.

Характеристический полином заданной матрицы имеет вид:

.

Собственные значения матрицы (корни характеристического уравнения) и собственные векторы равны:

Проекторы находим матричным произведением левых и правых собственных векторов. Для этого обратим матрицу и в качестве левых собственных векторов возьмем ее строки:

Векторное аналитическое решение имеет вид: