Реферат: Решение уравнений в целых числах

,

где - целое. Но тогда

,

и получаем

, .

Таким образом доказано, что всякое решение имеет вид (4). Остается еще проверить, что всякая пара чисел , получаемая по формулам (4) при целом , будет решением уравнения (3). Чтобы провести та кую проверку, подставим величины , в левую часть уравнения (3):

,

но так как - решение, то и, следовательно, , т.е. - решение уравнения (3), чем теорема полностью доказана.

Итак, если известно одно решение уравнения , то все остальные решения найдутся из арифметических прогрессий, общие члены которых имеют вид:

, .

3аметим, что в случае, когда , найденные раньше формулы решений

,

могут быть получены из только что выведенных формул , , если выбрать , что можно сделать, так как значения , являются, очевидно, решением уравнения

,

Как же найти какое-нибудь одно решение уравнения (3) в общем случае, когда . Начнем с примера.

Пусть дано уравнение

Преобразуем отношение коэффициентов при неизвестных.

Прежде всего, выделим целую часть неправильной дроби ;

Правильную дробь заменим равной ей дробью .

Тогда получим 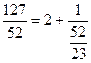. Проделаем такие же преобразования с полученной в знаменателе неправильной дробью .

Теперь исходная дробь примет вид:

Повторяя те же рассуждения для дроби получим .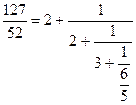

Выделяя целую часть неправильной дроби, придем к окончательному результату:

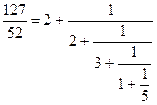
Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби - одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби :

, .

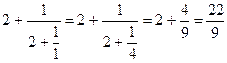Приведем полученное выражение к общему знаменателю и отбросим его, тогда

.

Из сопоставления полученного равенства с уравнением следует, что , будет решением этого уравнения и согласно теореме все его решения будут содержаться в прогрессиях , .

Полученный результат наводит на мысль о том, что и в общем случае для нахождения решения уравнения надо разложить отношение коэффициентов при неизвестных в цепкую дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были проведены выше.

Для доказательства этого предположения будут нужны некоторые свойства цепных дробей.