Реферат: Решение уравнений в целых числах

Отсюда следует, что

Если разложение в цепную дробь имеет звеньев, то п-я подходящая дробь совпадает с . Применяя равенство (8), при получим

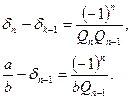(9)

Вернемся теперь к решению уравнения

, (10)

Перепишем соотношение (9) в виде .

Приводя к общему знаменателю и отбрасывая его, получим

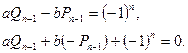
Умножим это соотношение на . Тогда

Отсюда следует, что пара чисел ,

, , (11)

является решением уравнения (10) и согласно теореме все решения этого уравнения имеют вид

,

Полученный результат полностью решает вопрос о нахождении всех целочисленных решений уравнения первой степени с двумя неизвестными. Перейдем теперь к рассмотрению некоторых уравнений второй степени.

3. ПРИМЕРЫ УРАВНЕНИЙ ВТОРОЙ СТЕПЕНИ С ТРЕМЯ НЕИЗВЕСТНЫМИ

П р и м е р I. Рассмотрим уравнение второй степени с тремя неизвестными:

(12)

Геометрически решение этого уравнения в целых числах можно истолковать как нахождение всех пифагоровых треугольников, т. е. прямоугольных треугольников, у которых и катеты , и гипотенуза выражаются целыми числами.

Обозначим через общий наибольший делитель чисел и : . Тогда

, ,

и уравнение (12) примет вид

.

Отсюда следует, что делится на и, значит, кратно : .

Теперь уравнение (12) можно записать в виде

;

сокращая на , получим

.

Мы пришли к уравнению того же вида, что и исход­ное, причем теперь величины и не имеют общих делителей, кроме 1. Таким образом, при решении уравнения (12) можно ограничиться случаем, когда и взаимно просты. Итак, пусть . Тогда хотя бы одна из величин и (например, ) будет нечетной. Перенося в правую часть уравнения (12), получим

; . (13)

Обозначим через общий наибольший делитель выражений и . Тогда

, , (14)

где и взаимно просты.

Подставляя в (13) значения и , получим

.

Так как числа и не имеют общих делителей, то полученное равенство возможно только в том случае, когда и будут полными квадратами:

, .

Но тогда

и

(15)

Найдем теперь и из равенств (14). Сложение этих равенств дает:

; . (16)

Вычитая второе из равенств (14) из первого, получим

; (17)

В силу нечетности из (15) получаем, что , и также нечетны. Более того, , так как иначе из равенств

и