Реферат: Решение уравнений в целых числах

Пусть, далее, - частное и - остаток от деления на Тогда , ; точно так же

Величины , ,… называются неполными частными. Приведенный выше процесс образования неполных частных называется алгоритмом Евклида. Остатки от деления , ,…удовлетворяют неравенствам

,

(5)

т. е. образуют ряд убывающих неотрицательных чисел.

Так как количество неотрицательных целых чисел, не превосходящих b, не может быть бесконечным, то на некотором шаге процесс образования неполных частных оборвется из-за обращения в ноль очередного остатка r. Пусть - последний отличный от нуля остаток в ряде (5); тогда и алгоритм Евклида для чисел a и b примет вид

(6)

Перепишем полученные равенства в виде

Заменяя значение в первой строке этих равенств соответствующим значением из второй строки значение - выражением из третьей, строки и т. д., получим разложение в цепную дробь:

Выражения, получающиеся из цепной дроби при отбрасывании всех ее звеньев, начиная с некоторого звена, назовем подходящими дробями. Первая: подходящая дробь получится при отбрасывании всех звеньев, начиная с : .

Вторая подходящая дробь получается отбрасыванием всех звеньев, начиная с : . Точно так же

и т. д.

В силу способа образования подходящих дробей возникают очевидные неравенства:

; .

Запишем k -ю подходящую дробь в виде ,

и найдем закон образования числителей и знаменателей подходящих дробей, Преобразуем первые подходящие дроби , , :

; , ;

; ; ;

;

;

Отсюда получаем:

; .

Применяя индукцию, докажем, что соотношения того же вида

, (7).

выполняются для всех .

Действительно, пусть равенства (7) выполняются для некоторого . Из определения подходящих дробей непосредственно следует, что при замене в выражении величины на перейдет в . Согласно индукционному предположению

.

Заменяя здесь на , получим:

.

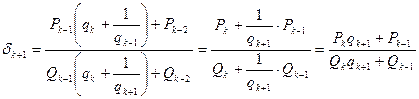Отсюда, так как , следует, что

, .

Таким образом, из выполнения равенств (7) для некоторого следует выполнение их для Но для равенства (7) - выполняется и, следовательно, их справедливость установлена для всех .

Покажем теперь, что разность соседних подходящих дробей удовлетворяет соотношению

. (8)

Действительно,

.

Пользуясь формулами (7), преобразуем числитель полученной дроби:

.

Выражение, стоящее в скобках, получается из исходного заменой на . Повторяя такие же преобразования для получающихся выражений, получим, очевидно, цепь равенств: