Академия ФСО России

Кафедра Физики

Тема: «Резистивные электрические цепи и методы их расчета».

Орел-2009

Содержание

Введение

Методы расчета простых резистивных цепей

Расчет резистивных электрических цепей методом токов ветвей

Метод узловых напряжений (МУН)

Заключение

Литература

ВВедение

Резистивными называются электрические цепи, в схему замещения которых входят только элементы активного сопротивления и источники. Чаще всего это цепи, составленные из резисторов. Основной особенностью резистивных цепей является отсутствие накопителей энергии – индуктивностей и емкостей. Поэтому в специальной литературе такие цепи часто называют цепями "без памяти".

Анализ резистивных цепей представляет собою простую задачу, так как колебания в резистивных цепях описываются линейными алгебраическими уравнениями. Полученные при рассмотрении резистивных цепей методы анализа колебаний и основные теоремы теории цепей в дальнейших темах будут распространены на цепи общего вида. В этом прежде всего ценность результатов анализа колебаний в резистивных цепях.

Методы расчета простых резистивных цепей

Простыми резистивными цепями называются такие цепи, элементы которых соединены или только последовательно, или только параллельно, или только последовательно и параллельно.

Параллельное (последовательное) соединение нескольких однотипных элементов может быть заменено одним элементом. Поэтому простую цепь с одним источником путем объединения элементов, включенных только параллельно или только последовательно, можно свести к цепи, содержащей лишь один элемент. Резистивные цепи, которые указанным путем не могут быть сведены к одному элементу активного сопротивления, называются сложными .

Расчет простых резистивных цепей с одним источником производится с использованием закона Ома. При наличии нескольких источников используется метод наложения.

Рассмотрим методы расчета простых цепей на примерах, употребляя для краткости термины "резистор" вместо термина "элемент активного сопротивления".

Параллельные цепи

Пусть электрическая цепь содержит два резистора и источник тока (рис. 1.1).

Рис. 1.1.

Определим напряжение в цепи и токи в ветвях, если значения сопротивлений резисторов и задающий ток источника известны. Учитывая заданное направление тока и выбранное направления токов и , составляем уравнение по первому закону Кирхгофа:

откуда

Для резисторов выбрана согласная система отсчетов и поэтому:

.

Тогда

Следовательно, эквивалентное сопротивление двух параллельно соединяемых резисторов определяется из соотношения:

,

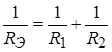и равно отношению произведения соединяемых сопротивлений к их сумме:

.

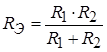--> ЧИТАТЬ ПОЛНОСТЬЮ <--