Реферат: Системы случайных величин
СВ X называется независимой от СВ Y , если закон распределения величины X не зависит от того, какое значение приняла СВ Y. В этом случае ![]() при любом y . Необходимо заметить, что если СВ X не зависит от СВ Y , то и СВ Y не зависит от СВ X . Для независимых СВ теорема умножения законов распределения имеет вид:
при любом y . Необходимо заметить, что если СВ X не зависит от СВ Y , то и СВ Y не зависит от СВ X . Для независимых СВ теорема умножения законов распределения имеет вид:
![]() .
.
Это условие рассматривается как необходимое и достаточное условие независимости СВ. Различают понятия функциональной и статистической зависимостей. При статистической зависимости нельзя указать точно значение, которое принимает одна из СВ, если известно значение другой, можно лишь определить влияние в среднем. Но по мере увеличения взаимозависимости статистическая зависимость превращается в функциональную.
5. Числовые характеристики системы двух СВ. Коррелированность
Как и для одной СВ, для системы двух СВ можно использовать начальные и центральные моменты.
Начальным моментом порядка k, s системы (X, Y ) называется МО произведения: ![]() ;
; ![]() .
.
Центральным моментом порядка k, s системы (X, Y ) называется МО произведения k -й и s -й степени соответствующих центрированных величин.
Для непрерывных СВ –
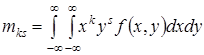 ,
,
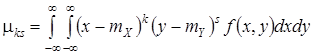 .
.
Первый начальный момент есть МО для соответствующей СВ X или Y .
Аналогично имеются и вторые центральные моменты системы СВ: ![]() и
и ![]() , которые характеризуют степень разбросанности случайной точки вдоль осей x и y соответственно.
, которые характеризуют степень разбросанности случайной точки вдоль осей x и y соответственно.
Особую роль в статистической радиотехнике играет второй смешанный центральный момент ![]() = KXY - корреляционный момент.
= KXY - корреляционный момент.
Для непрерывных СВ корреляционный момент выражается формулой
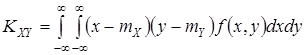 .
.
Этот момент, кроме рассеивания СВ, характеризует и взаимозависимость СВ X и Y . При этом, если СВ X и Y независимы, то ![]() . Докажем это предположение: если СВ X и Y независимы,
. Докажем это предположение: если СВ X и Y независимы, ![]() , то последний интеграл распадается на два независимых интеграла, в которых имеется произведение двух первых центральных моментов. Эти моменты равны нулю.
, то последний интеграл распадается на два независимых интеграла, в которых имеется произведение двух первых центральных моментов. Эти моменты равны нулю.
Чтобы исключить влияние разбросанности СВ на корреляционный момент, его делят на произведение среднеквадратических отклонений СВ X и СВ Y. Получается безразмерная величина, имеющая название "коэффициент корреляции": 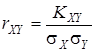 . Если СВ X и СВ Y независимы, то всегда
. Если СВ X и СВ Y независимы, то всегда ![]() Значит, независимые СВ всегда некоррелированы, однако обратное не всегда верно. Коррелированность характеризует не всякую взаимозависимость, а лишь линейную статистическую взаимозависимость. Это означает, что при возрастании одной СВ МО другой имеет тенденцию возрастать (или убывать) в среднем по линейному закону. Коэффициент корреляции характеризует степень разбросанности координат точки относительно линейной зависимости между X и Y. Если СВ X и Y имеют линейную функциональную зависимость, то коэффициент корреляции равен ±1, в зависимости от знака наклона этой функции. При этом говорят о положительной или отрицательной корреляции.
Значит, независимые СВ всегда некоррелированы, однако обратное не всегда верно. Коррелированность характеризует не всякую взаимозависимость, а лишь линейную статистическую взаимозависимость. Это означает, что при возрастании одной СВ МО другой имеет тенденцию возрастать (или убывать) в среднем по линейному закону. Коэффициент корреляции характеризует степень разбросанности координат точки относительно линейной зависимости между X и Y. Если СВ X и Y имеют линейную функциональную зависимость, то коэффициент корреляции равен ±1, в зависимости от знака наклона этой функции. При этом говорят о положительной или отрицательной корреляции.
Во многих радиотехнических устройствах имеются типовые радиотехнические тракты, состоящие из трех каскадно соединенных элементов: входной линейной цепи, нелинейного безынерционного элемента и выходной линейной цепи. В качестве этих элементов могут выступать различные электрические цепи с заданными характеристиками. На вход радиотехнического тракта воздействует аддитивная смесь сигнала и помехи:
![]() ,
,
где s (t ) - сигнал в виде гармонического или квазигармонического колебания; x (t ) - гауссов процесс с равномерной спектральной плотностью мощности (белый или квазибелый шум).
Известно [2], что в таких условиях при решении задачи обнаружения критерием качества работы устройства может служить отношение сигнал/помеха, которое определяется тремя выражениями:
система случайная величина
отношение сигнал/помеха по уровню 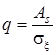 , где As - амплитуда сигнала;
, где As - амплитуда сигнала; ![]() - дисперсия шума;
- дисперсия шума;
отношение сигнал/помеха по мощности 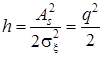 ;
;
энергетическое отношение сигнал/помеха 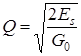 , где
, где ![]() - энергия сигнала;
- энергия сигнала; ![]() - спектральная плотность мощности помехи (белого или квазибелого шума).
- спектральная плотность мощности помехи (белого или квазибелого шума).
Если длительность сигнала ![]() , то
, то ![]() , а
, а 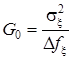 , где
, где ![]() - ширина энергетической полосы квазибелого шума.
- ширина энергетической полосы квазибелого шума.
Плотность вероятности сигнала (со случайной начальной фазой)
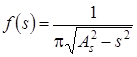 ,
, ![]() , а шума -
, а шума -  .
.
Если сигнал и помехи независимы, то ![]() , и плотность вероятности их смеси определяется интегралом свертки:
, и плотность вероятности их смеси определяется интегралом свертки:
 .
.