Реферат: Системы случайных величин
В статистической радиотехнике частот приходится иметь дело одновременно с несколькими случайными величинами, например, мгновенные значения напряжения на выходах антенной решетки при воздействии на ее вход сигналов и помех и т.д. Свойства системы нескольких СВ не исчерпываются свойствами отдельной СВ, так как при этом необходимо описание связи между составляющими системы СВ.
1. Функции распределения системы из двух случайных величин
Функцией распределения системы из двух СВ ![]() называется вероятность совместного выполнения двух неравенств
называется вероятность совместного выполнения двух неравенств ![]() и
и ![]() :
:
![]() .
.
По определению, функция распределения ![]() есть вероятность попадания случайной точки с координатами
есть вероятность попадания случайной точки с координатами ![]() в квадрат с бесконечными размерами, расположенный левее и ниже этой точки на плоскости
в квадрат с бесконечными размерами, расположенный левее и ниже этой точки на плоскости ![]() . Отдельно для каждой СВ X и Y можно определить одномерную функцию распределения, например,
. Отдельно для каждой СВ X и Y можно определить одномерную функцию распределения, например, ![]() есть вероятность попадания в полуплоскость, расположенную левее точки с координатой x . Также и
есть вероятность попадания в полуплоскость, расположенную левее точки с координатой x . Также и ![]() есть вероятность попадания в полуплоскость ниже точки y .
есть вероятность попадания в полуплоскость ниже точки y .
Свойства ![]() :
:
1) ![]() есть неубывающая функция обоих своих аргументов;
есть неубывающая функция обоих своих аргументов;
2) на - ¥ по обеим осям она равна нулю;
3) при равенстве +¥ одного из аргументов согласно другому аргументу она превращается в одномерную функцию распределения;
4) если оба аргумента равны +¥, то ![]() = 1.
= 1.
Вероятность попадания случайной точки в квадрат R с координатами ![]() по оси x и
по оси x и ![]() по оси y равна
по оси y равна
![]() .
.
![]() существует как для непрерывных, так и для дискретных СВ.
существует как для непрерывных, так и для дискретных СВ.
2. Двумерная плотность вероятности
Двумерная плотность вероятности есть предел следующего отношения:
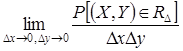 .
.
Если ![]() не только непрерывна, но и дифференцируема, то двумерная плотность вероятности
не только непрерывна, но и дифференцируема, то двумерная плотность вероятности ![]() есть вторая смешанная частная производная функции
есть вторая смешанная частная производная функции ![]() по x и по y .
по x и по y .
Размерность ![]() обратна произведению размерностей СВ X и Y.
обратна произведению размерностей СВ X и Y.
Таким образом, двумерная плотность вероятности есть предел отношению вероятности попадания точки в малый прямоугольник к площади этого прямоугольника, когда оба размера прямоугольника стремятся к нулю. Геометрически ![]() можно представить как некоторую поверхность.
можно представить как некоторую поверхность.
Если рассечь эту поверхность плоскостью, параллельной плоскости x 0y , и спроецировать полученное сечение на плоскость x 0y , то получится кривая, называемая "кривой равной плотности вероятности".
Иногда удобно рассматривать семейства кривых равной плотности при разных уровнях сечения. Как и для одномерной плотности вероятности, здесь вводится понятие элемента вероятности![]() .
.
Вероятность попадания случайной точки в произвольную область G определяется двумерным интегралом от ![]() по этой области. Геометрически это объем, ограниченный
по этой области. Геометрически это объем, ограниченный ![]() и областью G .
и областью G .
Если G есть прямоугольник с координатами вершин по оси x : ![]() и
и ![]() , а по оси y :
, а по оси y : ![]() и
и ![]() , то вероятность попадания случайной точки в этот прямоугольник определяется интегралом
, то вероятность попадания случайной точки в этот прямоугольник определяется интегралом
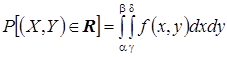 .
.
Свойства двумерной плотности вероятности:
![]() есть неотрицательная величина;
есть неотрицательная величина;
свойство нормировки аналогично одномерной плотности вероятности, но при двумерном интегрировании в бесконечных пределах.
3. Условные законы распределения отдельных СВ, входящих в систему СВ
Имея закон распределения системы двух СВ, всегда можно определить законы распределения отдельных СВ, входящих в систему. Например, ![]() и
и ![]() . Если известна плотность вероятности
. Если известна плотность вероятности ![]() , то
, то 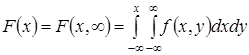 .
.
Аналогично определяется ![]() .
.
Таким образом, зная двумерную плотность вероятности, всегда можно определить одномерную плотность вероятности. Обратную задачу в общем случае решить невозможно. Ее можно решить, если известны условные плотности вероятности или функции распределения.
Условным законом распределения СВ, входящей в систему, называется ее закон распределения, определенный при условии, что другая СВ приняла определенное значение: ![]() . В этом случае можно найти двумерную плотность вероятности по формуле
. В этом случае можно найти двумерную плотность вероятности по формуле ![]() . Из этих выражений следует:
. Из этих выражений следует:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--