Реферат: Сліди і базиси розширеного поля
Мультиплікативною інверсією для ![]() є
є
![]()
Дійсно ![]() .
.
Нормальний базис (НБ) над полем ![]() визначається як множина сполучених елементів поля
визначається як множина сполучених елементів поля ![]() з підходящим вибором елемента
з підходящим вибором елемента ![]() . Розглянемо далі властивості НБ
. Розглянемо далі властивості НБ ![]() над полем
над полем ![]() . На елемент
. На елемент ![]() тут накладається необхідна умова:
тут накладається необхідна умова:![]() . Водночас
. Водночас ![]() не обов'язково має бути примітивним. У будь-якому полі
не обов'язково має бути примітивним. У будь-якому полі ![]() існує елемент зі слідом 1, тому в будь-якому полі
існує елемент зі слідом 1, тому в будь-якому полі ![]() існує і НБ. Елементи НБ можна подати
існує і НБ. Елементи НБ можна подати ![]() -вимірними векторами.
-вимірними векторами.
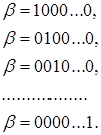
Зазначимо, що молодший розряд НБ звичайно записується ліворуч (на відміну від поліноміального, у якому молодший розряд прийнято записувати праворуч).
Кожен наступний елемент базису є циклічним зсувом вправо попереднього. Оскільки ![]() , елемент 1 поля
, елемент 1 поля ![]() визначається координатами
визначається координатами ![]() . Як бачимо, векторне подання елемента 1 поля
. Як бачимо, векторне подання елемента 1 поля ![]() в поліноміальному і нормальному базисах різні.
в поліноміальному і нормальному базисах різні.
Для порівняння двійкове подання елементів у поліноміальному і нормальному базисах подано в таблиці 3.
Таблиця 2 - Двійкове подання елементів у поліноміальному і нормальному базисах
| 0 | 0000 | 0000 | 1011 | 1110 | |
| 1 | 0001 | 1111 | 0101 | 0011 | |
| 0010 | 1001 | 1010 | 0001 | ||
| 0100 | 1100 | 0111 | 1010 | ||
| 1000 | 1000 | 1110 | 1101 | ||
| 0011 | 0110 | 1111 | 0010 | ||
| 0110 | 0101 | 1101 | 1011 | ||
| 1100 | 0100 | 1001 | 0111 |
Довільний елемент поля в нормальному базисі подається як
![]() .
.
Піднесення до квадрата елемента ![]() в нормальному базисі дає
в нормальному базисі дає

Таким чином, операція піднесення до квадрата (або витягу кореня квадратного) зводиться до циклічного зсуву вправо (або вліво) векторного подання елемента. Це одне з важливих технологічних переваг нормального базису перед поліноміальним. Іншою його перевагою є простота визначення сліду елемента. Дійсно:
![]() .
.
Отже, слід елемента дорівнює 0 при парній вазі його векторного подання в НБ і 1 – при непарній вазі. Ця властивість радикально спрощує визначення сліду елемента у НБ.
Наприклад: елемент ![]() у нормальному базисі має парну вагу векторного подання. Слід цього елемента дорівнює 0 Дійсно
у нормальному базисі має парну вагу векторного подання. Слід цього елемента дорівнює 0 Дійсно

На наступній лекції ми розглядатимемо окремо т.з. оптимальний нормальний базис, який має значні переваги у швидкості та технологічності обчислень.
Під час обчислення точок з багаторазовими операціями додавання (віднімання) і подвоєння більш продуктивними є групові операції не в афінних координатах, а різного роду проективних координатах. Це дозволяє уникнути обчислення оберненого елемента в полі як самої трудомісткої операції й заощадити тимчасові обчислювальні ресурси.
У стандартних проективних координатах проективна точка ![]() ,
, ![]() , відповідає афінній точці
, відповідає афінній точці ![]() Однорідне рівняння кривої після заміни змінних і множення на куб перемінної
Однорідне рівняння кривої після заміни змінних і множення на куб перемінної ![]() приймає вигляд
приймає вигляд
![]()
(в афінних координатах рівняння кривої має вигляд
![]() ).
).
Точка на нескінченності ![]() є вже одним з розв’язків даного рівняння. Зворотна точка тут, як і раніше, визначається інверсією знака
є вже одним з розв’язків даного рівняння. Зворотна точка тут, як і раніше, визначається інверсією знака ![]() координати
координати![]()
Подібно тому, як в афінних координатах, сумою точок ![]() і
і ![]() при
при ![]() називається точка
називається точка ![]() , координати якої (позначення
, координати якої (позначення ![]() надалі опускається для скорочення запису) рівні:
надалі опускається для скорочення запису) рівні:

де ![]()
Операцію підсумовування однакових точок ![]() називають подвоєнням, а координати точки
називають подвоєнням, а координати точки ![]() дорівнюють:
дорівнюють: