Реферат: Сліди і базиси розширеного поля

,

де

При подвоєнні точки кривої отримаємо

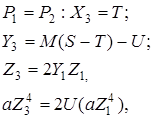
де

Нарешті, можна зробити наступні оцінки. Час виконання дорівнює і , де означає подання точки в модифікованих якобіанових координатах.

Формули, що визначають сумарне число інверсій ( ), множень і піднесень до квадрата при додаванні і подвоєнні точок відповідно в афінних , проективних , якобіанових координатах, координатах Чудновського і модифікованих якобіанових координатах наведені в таблиці 1 (узагальнення).

За деякими оцінками, одна інверсія , а піднесення до квадрата (при операціях у простому полі Галуа). Звідси стає зрозумілою доцільність переходу до проективних або до якобіанових координат, у яких операції інверсії відсутні.

Мінімальна обчислювальна складність додавання досягається за допомогою координат чудновського, а подвоєння – у модифікованих якобіанових координатах. Тому, звичайно, користуються змішаними координатами з метою оптимізації обчислень при багаторазовому додаванні точки.

Таблиця 3 - Число операцій множення , піднесення до квадрата й інверсій елементів простого поля при додаванні і подвоєнні точок у різних координатних системах

Координати	Додавання точок	Подвоєння точок
Афінні
Проективні
Якобіанові
Чудновського
Модифіковані Якобіанові

Після обчислення точки у змішаних координатах необхідно повернутися в афінні координати, для чого наприкінці обчислень потрібна одна інверсія.