Реферат: Случайные функции

и дисперсию

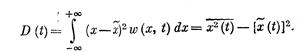
Среднее значение случайного процесса представляет собой некоторую среднюю кривую (ри с. 11.12), около которой группируются все возможные отдельные реализаци и этого процесса, а дисперсия D(t) или среднеквадратич­ное отклоне ние s (t) характеризуют рассеяние отдельных возможных реали­заций процесса около этой средн ей кривой.

Простейшим типом случайного процесса является чисто случайный процесс. В таком процессе все знач ен ия случайной величин ы в отдельные м омен­ты времени не зависят друг от друга. Тогда появления значений (x1,t1) и т. д. будут независимыми случай ны ми . собы тиями , дл я которых вероятность их совместного наступления равна, как известно, произведению вероятностей наступления каждого из них в отдельности. Следовательно, для чисто случайного процесса

и вообще

Это — самые простые соотношения в теории случайных процессов.Онимогут применяться для характеристики некоторых видов помех (чисто слу­чайные хаотические помехи).

Для характеристи ки полезных входных сигналов систем регулирования и следящих систем соотношения практи чески не могут при­меняться, так как для этих сигналов ход процесса в последующие моменты времени в какой-то степен и зависит от того, что было в предыдущие моменты времени,

Так, например, если речь идет о слежении за самолетом, то он не может как угодно быстро менять свое положение и скорость. Поэтому если он в мо­мент времени t занял положение х 1 то этим самым его возможное положение х 2 в следующий момент t2 ограничено, т. е. события (x1, t1) и ( x2 , t2) не будут независимыми. Чем более инерционен изучаемый объект, тем больше эта взаим озависимость, или корреляция. В таких случаях вместо формулы необходимо записать

где w2,1 1 { x2, t2)dх — условная вероятность того, что случайн ый процесс пройдет вблизи точки (x2, t2), есди он уже прошел через точку ( x1,t2). Сле­довательно, зная плотности вероятности, можно найти также и условную плотность вероятности

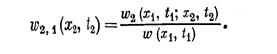
' Кроме того, имеет место следующая связь между основными плотно­стями вероятности:

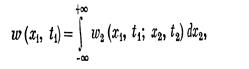
так как w (х 1, t1) есть плотность вероятности случайной величины (x1, t1) безотносительно к тому, какое потом будет значение (x2, t2), т. е. допус­кается —оо < х 2 < + оо. Аналогичным образом любая плотн ость вероят­ности низшего порядка всегда может быть получена из высшей , т. е. выс ­шие плотности вероятностей содержат наибольшее кол ичество инф ормации о случайном процессе (о взаимосвязях между возможными знач ениями слу­чайной величины х в различные моменты вр емени).

Написанные соотношения справедливы для случайных проц ессов любых типов. В зависимости же от того, до какого порядка принимают ся во внима­ние плотности вероятности, а также от разных дополнительных гипотез о фор­мах связи между w1, w2, . . ., wп рассматриваются разные типы случайных процессов в отличие от чисто случайных.

Стационарные случайные процессы

Стационарным случайным процессом называется такой процесс, вероят­ностные характеристики которого не зависят от времени. Все плотности ве­роятностей w1, w2, .. ., wn не меняются при любом сдвиге рассматриваемого участ­ка процесса во времени, т. е. при сохра­нении постоянной разности.

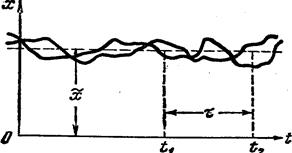
Можно сказать, что стационарный случайный процесс в какой-то мере аналогичен обычным стационарным иди уста­новившимся процессам в автоматических системах.. Например, при рассмотрении обычных установившихся периодических колебаний ничего не изменится, если пере­нести начало отсчета на какую-нибудь величину. При этом сохранят свои значения такие характеристики, как частота, амплитуда, среднеквадратич­ное значение и т. п.

В стационарном случайном процессе закон распределения один и тот же для каждого момента времени, т. е- плотность вероятности не зависит от времени: w(х, t) = w (x).

Отсюда получаем x`= соnst b s=const вдоль всего случайного процесса. Следовательно, в стационарном случайном процессе средняя линия, в отли­чие от общего случая будет прямая х` = соnst, подобно постоянному смещению средней линий обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном процессе определяемое s=const также будет все время одинаковым, подое­но постоянному значению среднеквадратичного отклонения обычных уста­новившихся колебаний от средней линии.

Аналогичным образом и двумерная плотность вероятности также будет одна и та же для одного и того же промежутка

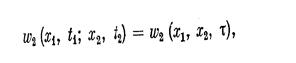
и также для n-мерной плотности вероятности.

Задание всех этих функций распределения плотности определяет слу­чайный процесс. Однако более удобно иметь дело с некоторыми осредненными и характеристиками процесса.

Прежде чем перейти к ним, отметим два важных для практики свойства. 1. Ограничиваясь только стационарными случайными процессами, можно будет определить только установившиеся (стационарные) динамиче­ские ошибки автоматических систем при случайных воздействиях. Такой прием применялся и ранее при рассмотрении регулярных воздействий, когда определялись динамические свойства систем регулирования по величине динамических ошибок в установившемся периодическом режиме.

2. Стационарные случайные процессы обладают замечательным свой­ством, которое известно под названием эргодической гипотезы.

Для стационарного случайного процесса с вероятностью, равной еди­нице (т. е. практически достоверно.