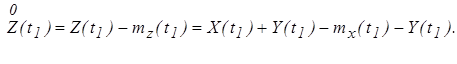Реферат: Случайные процессы в статической динамике

Корреляционная функция характеризует степень статистической взаимосвязи между двумя сечениями случайного процесса.

Взаимно корреляционная функция равна

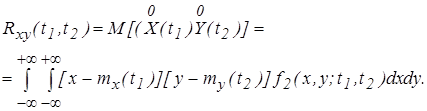(2.14)

Взаимно корреляционная функция характеризует степень статистической взаимосвязи между сечениями для двух процессов.

Для Гаусcовских случайных процессов определяющей характеристикой является двумерная плотность вероятности, поэтому корреляционная функция полностью характеризуют статистические свойства случайного процесса.

Для стационарных процессов корреляционная функция зависит от разности аргументов t = t2 –t1

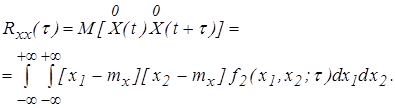(2.15)

При этом дисперсия равна

.(2.16)

Для эргодических процессов

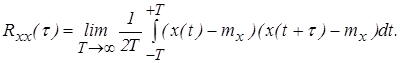(2.17)

2.3 Основные свойства корреляционной функции

1. Начальное значение корреляционной функции равно дисперсии

.(2.18)

2. Значение Rx(t) при любом t не может превышать ее начального значения

(2.19)

3. Корреляционная функция симметрична относительно своих аргументов

(2.20)

.

Для взаимно корреляционных функций это не справедливо

4. Корреляционная функция стационарных процессов является четной функцией, а взаимно корреляционная – нечетной

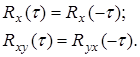(2.21)

5. Корреляционная функция суммы Z(t) = X(t)+Y(t), где X(t) и Y(t) – случайные процессы

(2.22)

6. Корреляционная функция произведения Z(t) = X(t)Y(t), где X(t)–случайный процесс, а Y(t) - неслучайная помеха

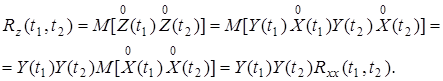(2.23)

7. Корреляционная функция суммы Z(t) = X(t)+Y(t), где X(t) – случайный процесс, а Y(t) – неслучайная функция

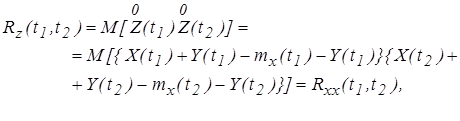(2.24)

так как