Реферат: Соответствие между молекулами и группами симметрии

b_k = S а_kj a_j k,j=1,2,3... .3N

Это преобразование может быть просто поворотом системы на некоторый угол. Существует также обратное преобразование:

a_i = S (а_in ) - ¹ b_n i,n=1,2,3... .3N

Если координаты смещений атомов a_i при преобразовании R переходят в координаты a_i ` и описываются таким преобразованием:

a_k ` = S R_kj a_j k,j=1,2,3... .3N ,

то новые координаты b_k ` можно получить:

b_k `= S а<sub>kj</sub> a<sub>j</sub> `= S а_ij R_ji a_i = Sa_kj SR_ji (a_in ) - ¹ a_n = S ( S а_kj R_ji (a_in ) - ¹ ) b_n

Когда два представления отличаются только тем, что базисные координаты одного являются линейными комбинациями координат другого, говорят, что представления эквивалентны, т.е. представление R_ji эквивалентно представлению Sа_ki R_ji (а_in ) - ¹ . Эквивалентность представлений может быть установлена на основании того, что соответствующие представления имеют одинаковый spur , или характер, т.е. величина

c (R) = SR_ii =R₁₁ +R₂₂ +R₃₃ +... +R_3N3N

постоянна для данного преобразования симметрии R . Легко показать, что преобразования, соответствующие эквивалентным представлениям имеют одинаковые характеры представлений.

c ( R) = S [ a_mi R_ik ( a_km ) - ¹ ] = R_ik [ a_mi ( a_km ) - ¹ ] = R_ik d _ki = R_ii = c ( R)

Для линейного преобразования к новым координатам справедливо (а_km ) - ¹ a_mi = d_ki .

Предположим, что мы каким-то образом нашли преобразование от декартовых координат смещения X, Y, Z к нормальным координатам Q_i . Известно, что в этом случае координаты при преобразованиях симметрии не смешиваются, а потенциальная и кинетическая энергии имеют вид квадратичной функции:

,

Координаты с двумя значками вырождены f_k раз. Существует f_k таких колебаний с частотой l_i ^1/2 . f_k - степень вырождения. Если теперь мы применим к молекуле операцию симметрии R она не может влиять на физическое состояние молекулы, поскольку Т и V являются инвариантными относительно любого преобразования группы симметрии молекулы.

Поэтому единственный эффект, который может произвести это преобразование R на невырожденную координату Q_i - это либо оставить ее неизменной, либо сменить знак на обратный, т.е.

RQ_i = cQ_i .

Это же видно из квадратичной формы V и T . Вырожденные переменные Q_{k a} определяются неоднозначно, они перемешиваются между собой, но ортогональные их комбинации остаются нормальными координатами. Условия инвариантности V и T будут удовлетворены, если R преобразует каждую Q_{k a} в комбинацию всех координат, соответствующих одной и той же частоте l_k ^1/2 .

RQ_{k a} = Sа _{k a b} Q_{k b (} k=1,2,..., f_k ).

Поэтому представление данной операции группы симметрии будет выглядеть так:

Т.о. представление в нормальных координатах будет иметь самый простой вид. Вообще, новая система координат может быть выбрана так, что преобразование, представляющее любую операцию симметрии будет выглядеть диагональным:

,

т.е. всякая координата будет преобразовываться в себя с некоторым множителем. Но не всегда можно найти такую систему координат, чтобы каждое преобразование группы имело самый простой вид, но нельзя одновременно это сделать со всеми преобразованиями R . Однако обычно можно найти такую систему координат, в которой будут значительно упрощены все преобразования группы. Тогда, очевидно, группы определенных координат не будут смешиваться при любых преобразованиях группы. В такой системе координат представления наиболее простые и называются они неприводимыми представлениями. Для описания неприводимых представлений мы воспользовались концепцией нормальных координат в качестве конкретного примера. Однако, следует помнить, эта концепция неприводимых представлений совершенно не зависит от представления о нормальных координатах или проблемы молекулярных колебаний. Она появляется всякий раз, когда система линейных преобразований имеет свойства группы.

Итак, если имеется представление в виде матрицы Г (R) =|а_i |; |а_ik |=0 , то часто возможно найти преобразование координат такое, что все матрицы будут иметь форму:

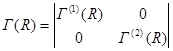
Тогда представление Г (R) называется приводимым, а Г ^{(1) (} R) и Г ^{(2) (} R) - неприводимыми, если их невозможно далее упростить. h операций группы могут действовать на любое число i переменных k_i (молекулы с разным числом атомов). Полное представление группы по отношению к этим переменным будет состоять из матриц с i строками и i столбцами. Если мы напишем такую матрицу в приведенной форме, некоторые из матриц неприводимых представлений могут появиться более чем один раз (некоторые могут не появиться совсем), т.к число i не зависит от группы. Символически это обозначают так:

Г (R) =S n ⁽ⁱ⁾ Г ^{(i) (} R),

где n ⁽ⁱ⁾ дает число раз, которое неприводимое представление Г ^{(i) (} R) содержится в приводимом Г (R). Можно символически записать то же самое для любой операции R группы т.е.: