Реферат: Спектральная теория операторов
1.2 Линейные преобразования
Определение 1.2 Графиком G(T) линейного преобразования Т называется подпространство в произведении подпространств Н1 ![]() Н2 , образованное по правилу
Н2 , образованное по правилу
G(T) =![]() (1.2).
(1.2).
Определение 1.3 Линейное преобразование Т называется замкнутым, если его график функции замкнут в Н3 . Иначе замкнутость оператора Т можно определить так: пусть xn ![]() D(T), xn
D(T), xn ![]() x, Tхn
x, Tхn ![]() у. Тогда x
у. Тогда x ![]() D(Т) и Тх = у.
D(Т) и Тх = у.
Отметим, что, как правило, дифференциальные операторы замкнуты. Этот факт и определяет необходимость рассмотрения класса замкнутых операторов.
Определение 1.4 Линейное преобразование Т называется ограниченным, если D = Н1 и
sup![]() =M<
=M<![]() (1.3).
(1.3).
Определение 1.5 Нормой линейного ограниченного преобразования T называется число
![]() sup
sup![]() (1.4)
(1.4)
Линейное преобразование ограничено, если оно непрерывно в начале координат. Тогда оно непрерывно в каждой точке. Ограниченное линейное преобразование, очевидно, непрерывно.
Пусть Т1 , Т2 — линейные ограниченные операторы, отображающие пространство Н1 в Н2 . Тогда ясно, что сумма T1 +Т2 также является линейным ограниченным оператором. Кроме того,
![]() (1.5)
(1.5)
В силу определения (![]() T)x=
T)x= ![]() Тх, где
Тх, где ![]() элемент поля скаляров, следовательно, оператор
элемент поля скаляров, следовательно, оператор ![]() Т ограничен, если T ограничен. Следовательно, множество всех линейных ограниченных операторов образует линейное пространство, а норма оператора является нормой на этом пространстве. Полученное таким образом линейное нормированное пространство операторов обозначается через L(H1 ,H2 ). Нетрудно показать, что пространство L(H1 ,H2 ) полно. Действительно, если {Tn} — последовательность Коши этого пространства, то для любого элемента х пространства H1 имеем
Т ограничен, если T ограничен. Следовательно, множество всех линейных ограниченных операторов образует линейное пространство, а норма оператора является нормой на этом пространстве. Полученное таким образом линейное нормированное пространство операторов обозначается через L(H1 ,H2 ). Нетрудно показать, что пространство L(H1 ,H2 ) полно. Действительно, если {Tn} — последовательность Коши этого пространства, то для любого элемента х пространства H1 имеем
![]() (1.6).
(1.6).
Следовательно, {Tn x} является последовательностью Коши пространства H2 , ее предел обозначим через Тх. Очевидно, что оператор Т линеен и ограничен. Если n>N(e) и ![]()
![]() , то
, то
![]()
![]()
![]() +
+![]()
![]() (1.7).
(1.7).
1.3 Сопряжённый и самосопряжённый оператор
Определение 1.6 Пусть T — линейный ограниченный оператор из H1 в Н2 сопряженный оператор T* (определенный на Н2 и принимающий значения в Н.) определяется условием у = Т*х в том и только том случае, если существует вектор у такой, что [y,z] = [x,Tz] для любого z ![]() H1 .
H1 .
Определение 1.7 Пусть H1 =H2 =H. Оператор L c плотной областью определения, называется самосопряжённым, если L=L* [9].
2 Спектральная теория операторов
2.1 Спектр оператора
В приложениях часто возникает следующая задача: задан оператор Т, найти элемент х такой, что Тх =у, где элемент у задан. В общем случае множество решений может оказаться либо пустым, либо содержать слишком много элементов. Можно рассмотреть несколько более общую задачу: найти элемент х такой, что ![]() х—Тх=у, где
х—Тх=у, где ![]() — скаляр. Важность рассмотрения этой задачи обусловлена тем, что последняя тесно связана со структурой самого оператора. Возможно, что читатель имеет представление о собственных значениях и собственных векторах матрицы. Спектральная теория операторов рассматривает вопросы, связанные с этими понятиями, но уже для более широкого класса операторов. В дальнейшем гильбертовы пространства рассматриваются над полем комплексных чисел.
— скаляр. Важность рассмотрения этой задачи обусловлена тем, что последняя тесно связана со структурой самого оператора. Возможно, что читатель имеет представление о собственных значениях и собственных векторах матрицы. Спектральная теория операторов рассматривает вопросы, связанные с этими понятиями, но уже для более широкого класса операторов. В дальнейшем гильбертовы пространства рассматриваются над полем комплексных чисел.
Определение2.1 Пусть Т — замкнутый линейный оператор, отображающий пространство Н в себя. Комплексное число ![]() называется собственным значениемоператора Т, если существует элемент х. из Н такой, что Тх =
называется собственным значениемоператора Т, если существует элемент х. из Н такой, что Тх = ![]() х; при этом элемент х (предполагается, что его норма равна 1) называется собственным вектором, соответствующим
х; при этом элемент х (предполагается, что его норма равна 1) называется собственным вектором, соответствующим ![]() . Множество всех собственных значений оператора Т образует его точечный спектр [4].
. Множество всех собственных значений оператора Т образует его точечный спектр [4].
Если комплексное число X не принадлежит точечному спектру оператора Т, то, безусловно, можно определить оператор (![]() I– T)-1 (здесь I — тождественный оператор): х = (
I– T)-1 (здесь I — тождественный оператор): х = (![]() I— Т)
I— Т)![]() yв том и только том случае, если у =
yв том и только том случае, если у =![]() –Тх.
–Тх.
Обратный оператор (![]() I—Т)
I—Т)![]() очевидно, линеен. Однако для наших целей весьма важно знать условия, при выполнении которых обратный оператор (
очевидно, линеен. Однако для наших целей весьма важно знать условия, при выполнении которых обратный оператор (![]() I –Т)
I –Т)![]() кроме того и непрерывен. Для этого необходимо, чтобы множество значений оператора (
кроме того и непрерывен. Для этого необходимо, чтобы множество значений оператора (![]() I —Т) совпадало со всем пространством H. Но самое замечательное при этом заключается в том, что для замкнутых операторов это условие оказывается и достаточным, и этим в значительной степени объясняется наш интерес к замкнутым операторам.
I —Т) совпадало со всем пространством H. Но самое замечательное при этом заключается в том, что для замкнутых операторов это условие оказывается и достаточным, и этим в значительной степени объясняется наш интерес к замкнутым операторам.
Теорема 2.1 Пусть Т — замкнутый линейный оператор и число ![]() не принадлежит его точечному спектру. Пусть, далее, множество значений оператора (
не принадлежит его точечному спектру. Пусть, далее, множество значений оператора (![]() I— Т) совпадает со всем пространством Н. Тогда оператор (
I— Т) совпадает со всем пространством Н. Тогда оператор (![]() I—T)-1 ограничен, т. е. для любого элемента х из Н и некоторого числа М (зависящего от
I—T)-1 ограничен, т. е. для любого элемента х из Н и некоторого числа М (зависящего от ![]() ) справедлива оценка
) справедлива оценка
![]()
![]() (2.1).
(2.1).
Доказательство. Оператор ( ![]() I —T)
I —T)![]() замкнут и его область определения есть все пространство Н. Следовательно, по теореме о замкнутом графике он должен быть непрерывным.
замкнут и его область определения есть все пространство Н. Следовательно, по теореме о замкнутом графике он должен быть непрерывным.
Определение2.2 Множество комплексных чисел ![]() , не являющихся собственными значениями оператора Т, таких, что множество значений оператора
, не являющихся собственными значениями оператора Т, таких, что множество значений оператора ![]() I — Т совпадает со всем пространством Н, называется резольвентным множествомоператора Т и обозначается через p (Т). Для
I — Т совпадает со всем пространством Н, называется резольвентным множествомоператора Т и обозначается через p (Т). Для ![]()
![]() р(T) оператор (
р(T) оператор ( ![]() I — Т)-1 обозначается через R (
I — Т)-1 обозначается через R ( ![]() , T ) и называется резольвентой Т.Дополнение резольвентного множества называют спектромоператора. Таким образом, точечный спектр оператора является подмножеством его спектра [5].
, T ) и называется резольвентой Т.Дополнение резольвентного множества называют спектромоператора. Таким образом, точечный спектр оператора является подмножеством его спектра [5].
Пример 2.1. Пусть H = L 2 (0, 1),aD — класс функций, производные которых тоже принадлежат L2 (0, 1). Для функций f![]() Dположим Tf =
Dположим Tf = ![]() . Тогда оператор Т замкнут и его область определения плотна. Рассмотрим его резольвентное множество. Уравнение
. Тогда оператор Т замкнут и его область определения плотна. Рассмотрим его резольвентное множество. Уравнение ![]() f —
f —![]() = 0 означает, что f ( t )= f (0) e
= 0 означает, что f ( t )= f (0) e![]() и e
и e![]()
![]() L2 (0, 1). Таким образом, все числа
L2 (0, 1). Таким образом, все числа![]() принадлежат спектру оператора T, и потому его резольвентное множество пусто. Этого, однако, не может быть для ограниченных операторов.
принадлежат спектру оператора T, и потому его резольвентное множество пусто. Этого, однако, не может быть для ограниченных операторов.
2.2 Понятие об ограниченном операторе
Теорема 2.2 Пусть Т — ограниченный оператор, отображающий пространство Н в себя. Тогда ![]()
![]() р(T), если |
р(T), если |![]() |>r, где r = lim
|>r, где r = lim![]()
![]() . Число г>0 называется спектральным радиусом оператора Т [5]
. Число г>0 называется спектральным радиусом оператора Т [5]
Доказательство.Основной шаг заключается в доказательстве сходимости ряда
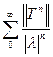 (2.2)
(2.2)
для всех |![]() |>г. Это непосредственно следует из того факта, что мажорирующий ряд
|>г. Это непосредственно следует из того факта, что мажорирующий ряд
![]() (2.3)
(2.3)
абсолютно сходится при |z|>lim![]() . Следовательно, ряд сходится по норме пространства L(H,H). Более того, имеем так что
. Следовательно, ряд сходится по норме пространства L(H,H). Более того, имеем так что
(![]() I – T)(
I – T)(![]() )=(
)=(![]() )(
)(![]() – T)=(
– T)=(![]() ) (2.4)
) (2.4)