Реферат: Спектральная теория операторов

Доказательство. Сначала докажем, что резольвентное множество произвольного замкнутого оператора открыто. В слу­чае, если резольвентное множество замкнутого оператора пусто, то доказывать нечего. Предположим, что резольвентное множе­ство не пусто и содержит число ₀ . Покажем, что все , удов­летворяющие условию |–₀ |/||R(₀ ; T )\\ < 1, принадлежат ре­зольвентному множеству. Прежде всего, отметим, что для таких ряд (–₀ )^п R (₀ ; Т)^п сходится и

(I+ (–₀ ) R (₀ ; T)) = (₀ –)R (₀ ; Т)^п (2.5).

Докажем, что

(2.6)

Пусть xH. Имеем

( I – T ) ()x=x (2.7).

Если xD(T), то

(2.8).

Таким образом, оператор R ( λ ; T ) — резольвента. Следовательно, резольвентное множество открыто. Более того, имеем

R ( )= (2.9)

при ||λ R (λ₀ ; T )||< 1.

Таким образом, если L(∙) — линейный непрерывный функ­ционал на L ( H , H ), то функция L ( R ( K ; T )) оказывается анали­тической на резольвентном множестве оператора Т. Рассмотрим теперь случай, когда оператор Т ограничен. Предположим, что его спектр — пустое множество. Тогда для любого линейного непрерывного функционала L (∙) аналитическая функция L ( R (λ;Т)) определена на всей комплексной плоскости и, кроме того, она ограничена в бесконечности, поскольку ||λR (λ; Т) ||≤(1–/λ)-¹ для всех |λ|>||Т||. Следовательно, в силу клас­сической теоремы Лиувилля для любого функционала L (∙) и любого комплексного λ функция L ( R (λ;Т)) тождественно равна пулю. НотогдаL(I)=L(λR(λ;T)–TR(λ; I)) = L(TR(λ; T )). Поэтому в силу сходимости правой части последнего равенства к нулю при λ→ +L ( I ) = 0 для любого линейного непрерыв­ного функционала L (∙), что невозможно. Таким образом спектр ограниченного оператора не может быть пустым.

Определение 2.3 Ограниченный оператор называется квазинильпотентным,если его спектральный радиус равен нулю [6].

Спектр квазинильпотентного оператора содержит лишь ну­левую точку.

Пример2.2 Пусть H = L ₂ (0, 1). Определим оператор Т соотношениями

Tf = g, g(t)=f(s)ds , 0t1 (2.10)

Тогда оператор Т линеен и ограничен. Используя неравенство Шиарца,найдем Что касается спектра оператора T,то заметим, что если

λf ( t )— f ( s ) ds = 0 почти всюду на [0, 1],

f — непрерывная функция. Далее, уравнение

λ f ( t )- f ( s ) ds = g ( t )

имеет единственное решение

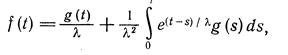(2.11)

и потому спектр оператора Т может содержать лишь нулевую точку. Это можно доказать заметив, что оператор Т квазиниль-потентен:

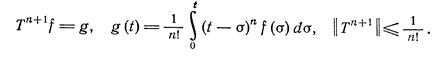(2.12)

Как было доказано выше, спектр ограниченного оператора не может быть пустым. Следовательно, спектр оператора Т состоит из нулевой точки. С другой стороны, в рассматриваемом случае, нуль не является собственным значением, поскольку из условия Tf = 0 следует, что f = 0. Отсюда следует, что Т^-1 — замкнутый линейный оператор, однако он неограничен. Это и следовало ожидать, поскольку T^-1f = g означает, что g = f '.

Пример 2.3 В общем случае нельзя указать эффектив­ной процедуры отыскания спектра и резольвентного множества заданного оператора. Однако, для интегральных операторов та­кой общий метод существует; он заключается в дифференциро­вании необходимое число раз равенства, определяющего точку спектра с целью получения определяющего дифференциального уравнения. Рассмотрим, например, оператор

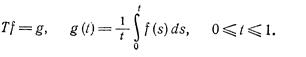(2.13)

Рассмотрим сначала точечный спектр этого оператора. Если функция L(•) из H является собственным вектором, то

f ( s ) ds = λtf ( t ) почти всюду.

Дифференцируя обе части этого равенства, получим дифферен­циальное уравнение

f ( t ) = + ( t ) ;

его общее решение имеет вид f ( t )= k - t^a , где k — произвольное постоянное число, а а = (1 –λ)/λ.С другой стороны, из усло­вия