Реферат: Статистическая обработка экспериментальных данных

при n = 23;

Сравниваем с : . Отбрасываем измерение №11 и повторяем вычисления.

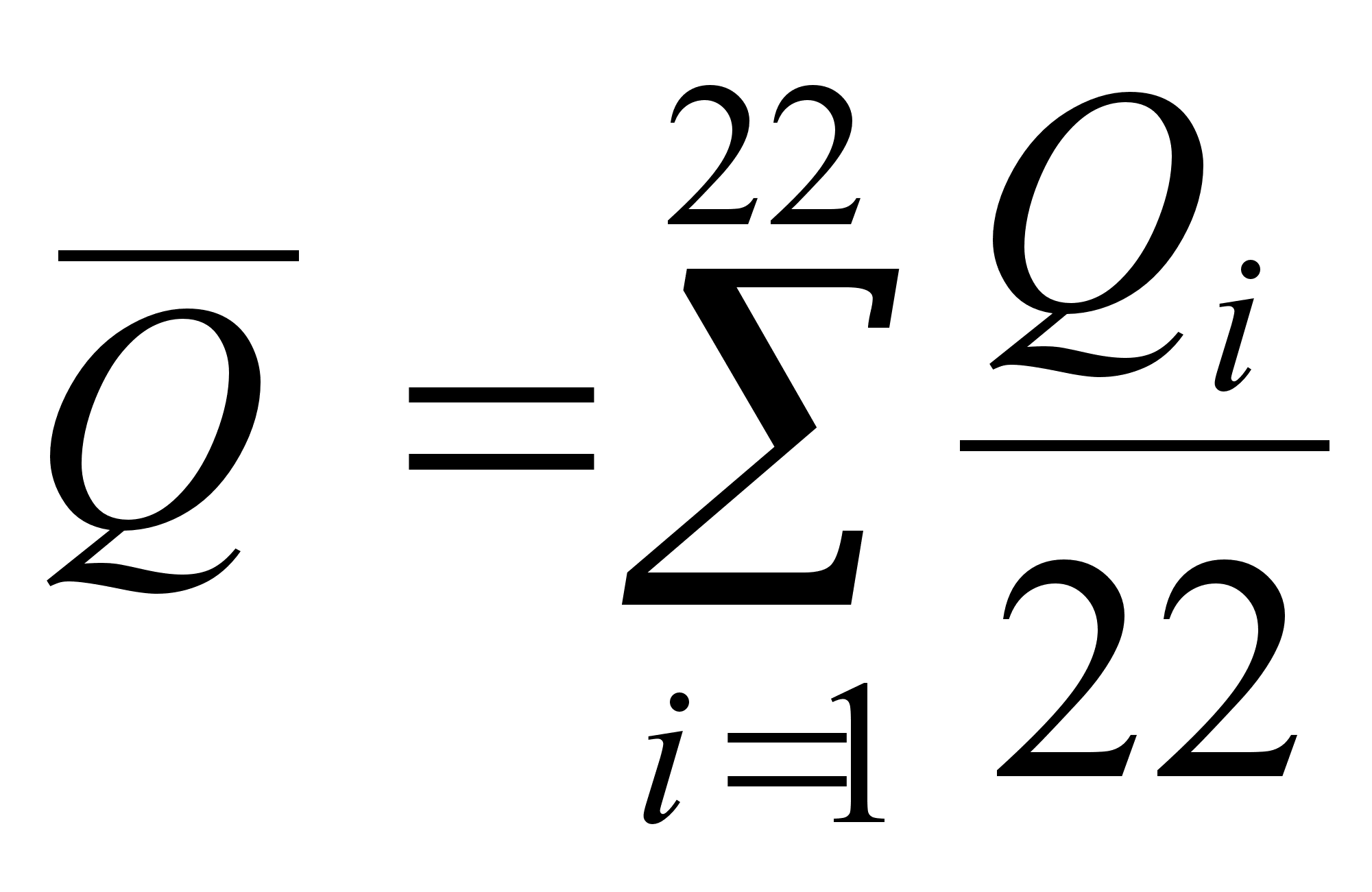
(8)

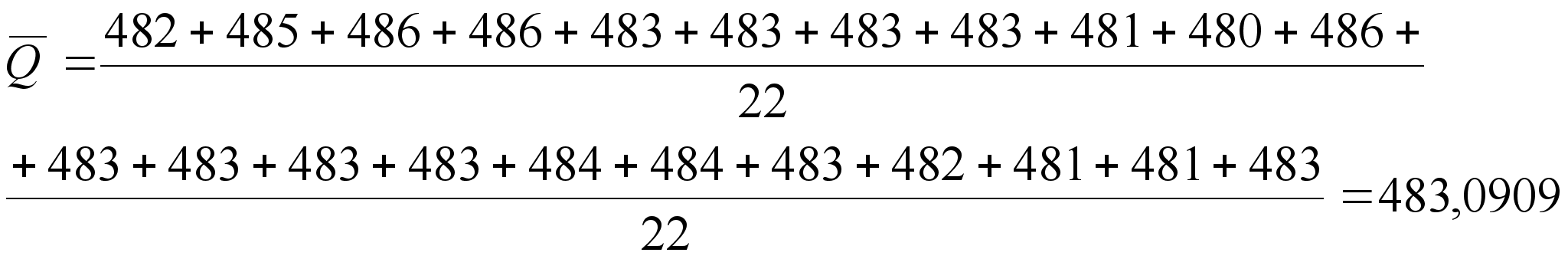
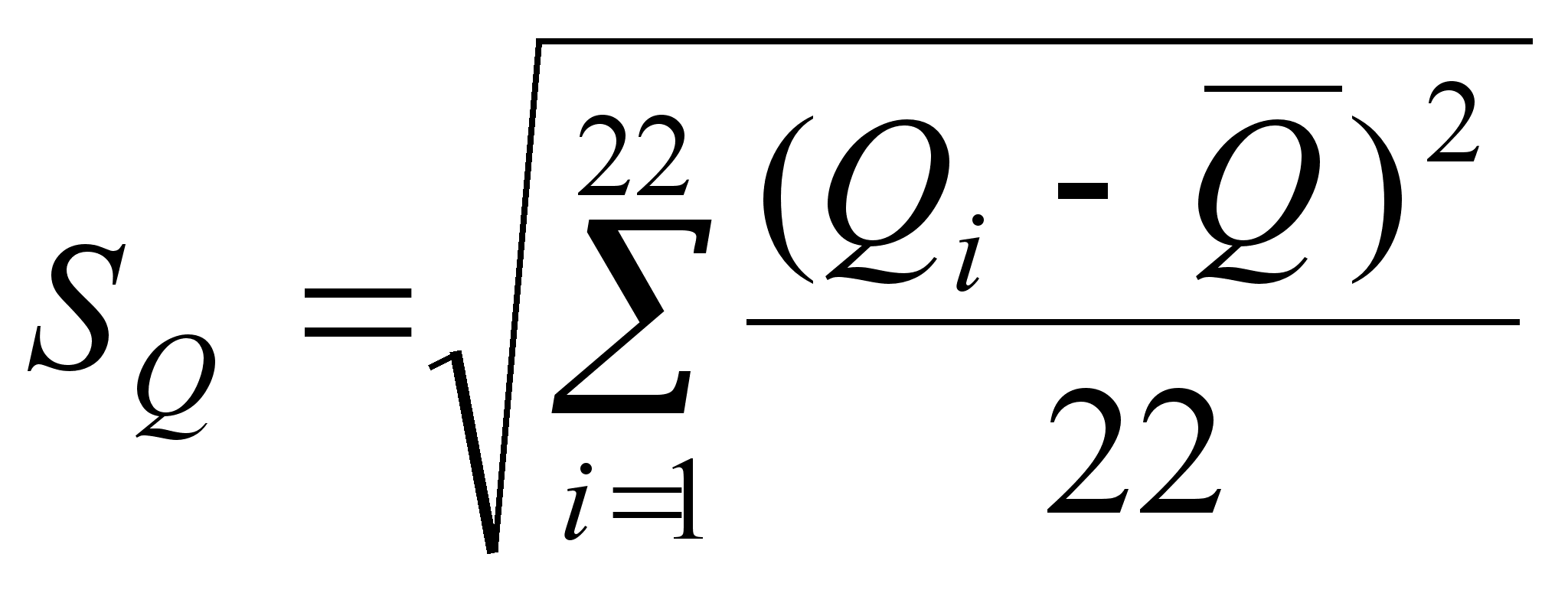(9)

Таблица 4

№ из-мерения	Результат измере-ния (Qi)			№ из-мерения	Результат измере-ния (Qi)
1	482	-1,0909	1,1901	12	483	-0,0909	0,0083
2	485	1,9091	3,6446	13	483	-0,0909	0,0083
3	486	2,9091	8,4628	14	483	-0,0909	0,0083
4	486	2,9091	8,4628	15	483	-0,0909	0,0083
5	483	-0,0909	0,0083	16	484	0,9091	0,8264
6	483	-0,0909	0,0083	17	484	0,9091	0,8264
7	483	-0,0909	0,0083	18	483	-0,0909	0,0083
8	483	-0,0909	0,0083	19	482	-1,0909	1,1901
9	481	-2,0909	4,3719	20	481	-2,0909	4,3719
10	480	-3,0909	9,5537	21	481	-2,0909	4,3719
11	486	2,9091	8,4628	22	483	-0,0909	0,0083
				Σ		0	55,8182

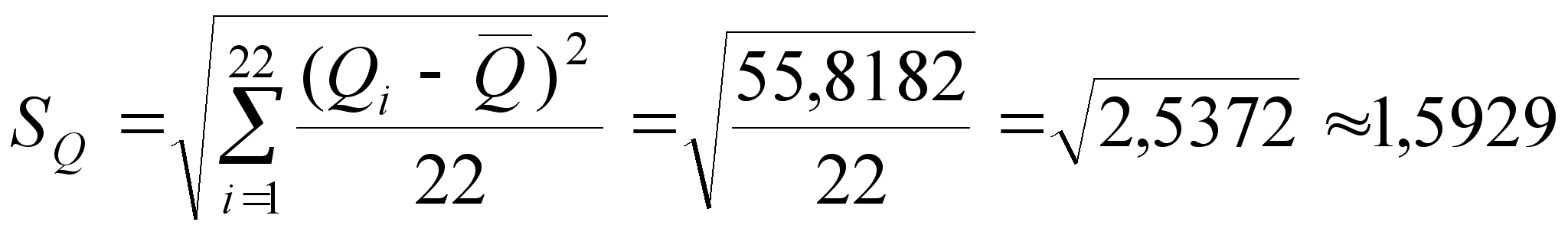
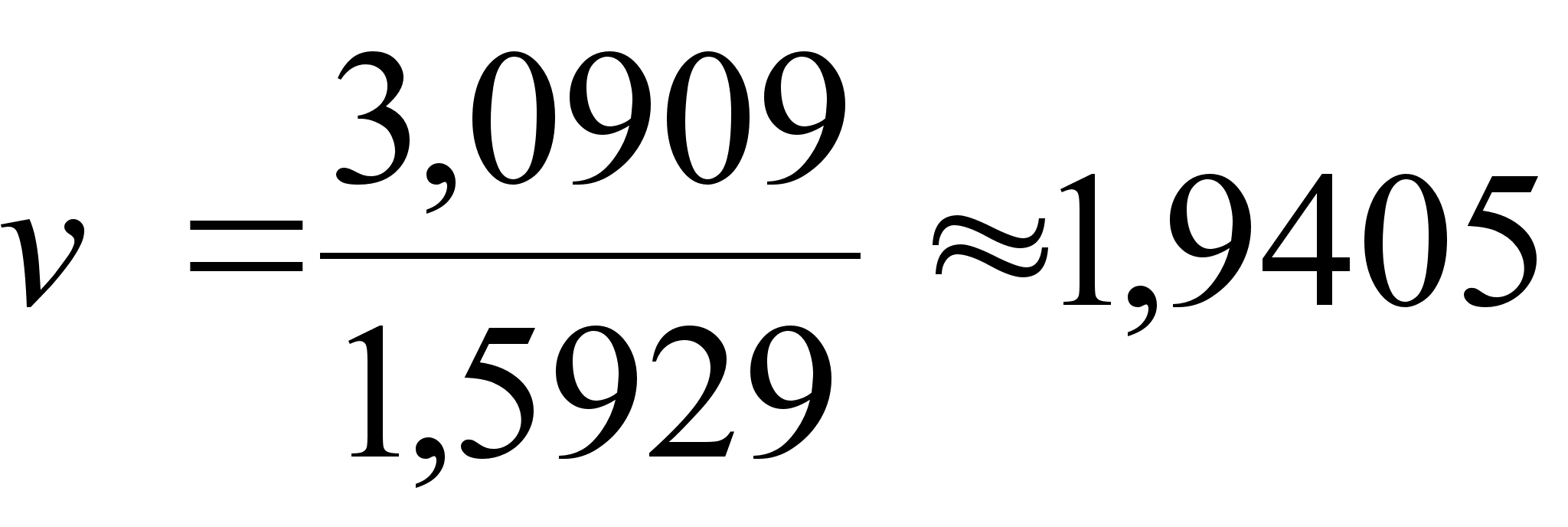
при n = 22;

Сравниваем с . Так как , то результат измерения №10 не является ошибочным и окончательно остается 22 измерения, т.е. n = 22.

3. Проверяем гипотезу о нормальности распределения оставшихся результатов измерений.

– Применяем критерий 1, вычисляем отношение

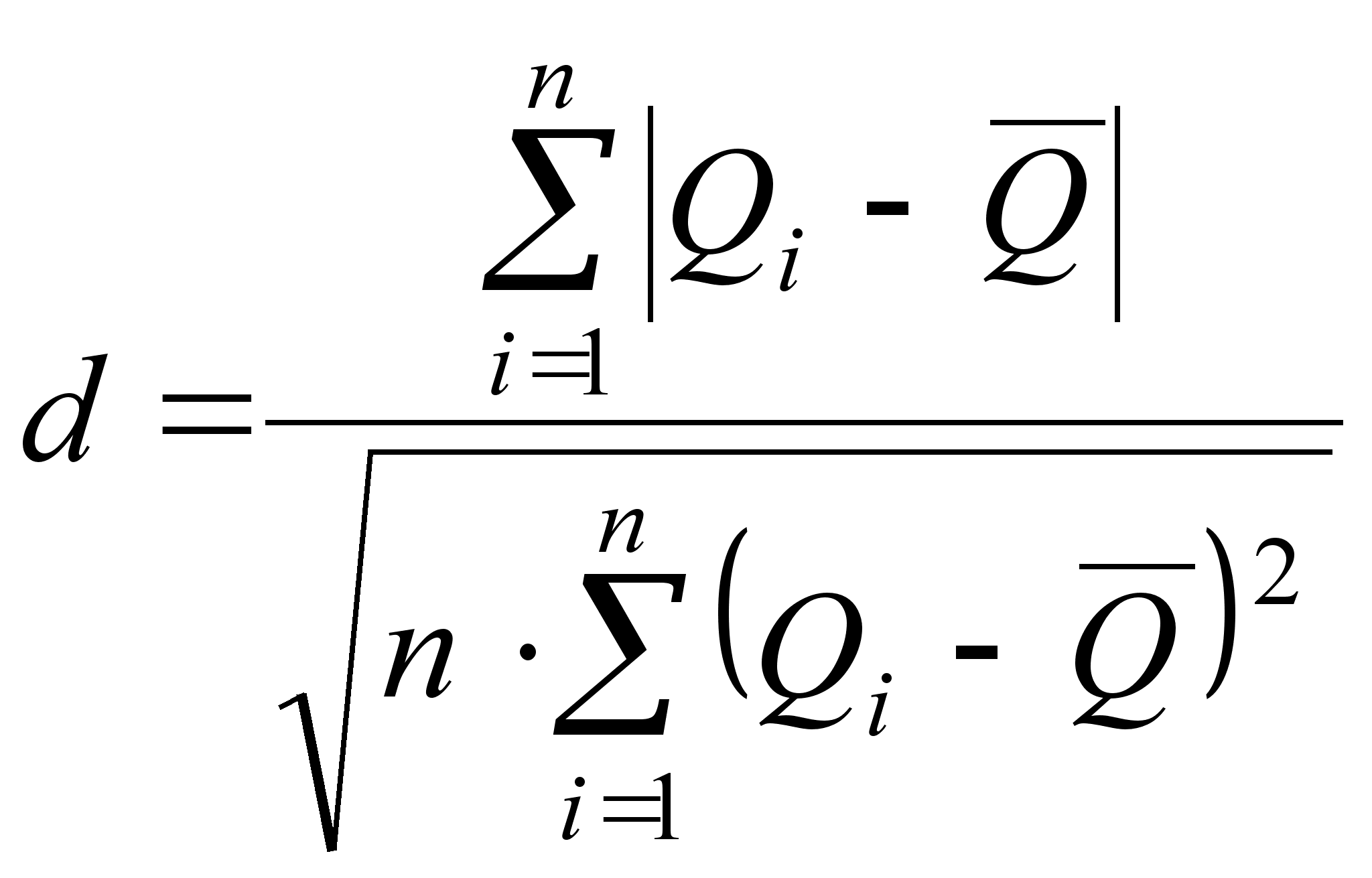(10)

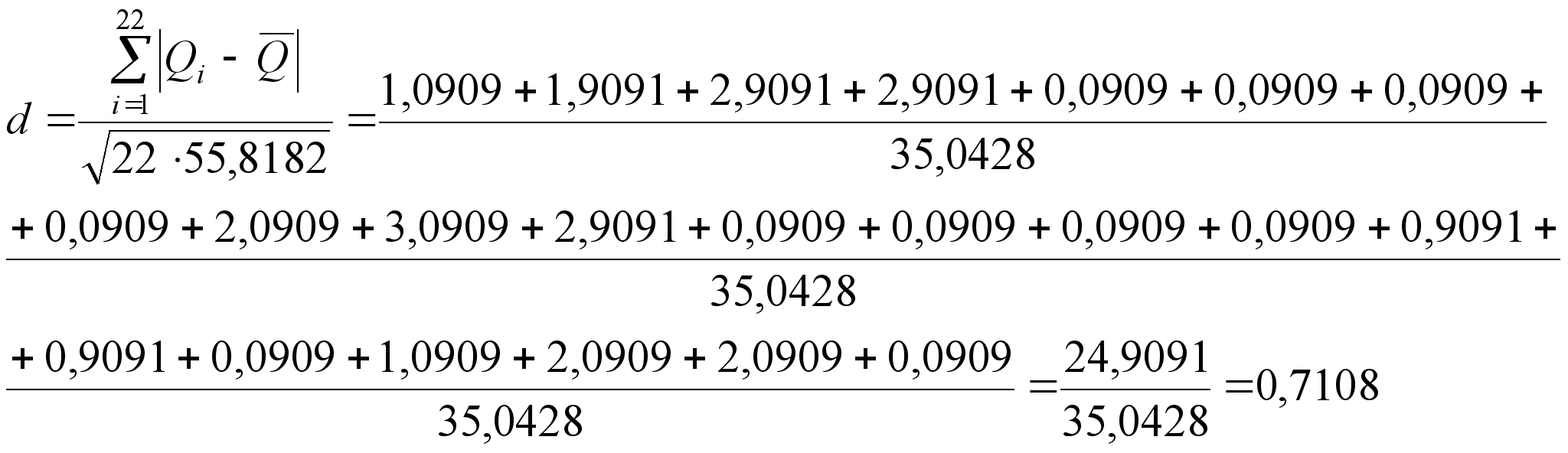
– задаемся доверительной вероятностью P₁ = 0,99 и для уровня значимости q₁ = 1 – P₁ по таблице П7 определяем квантили распределения и , , для n = 22.

– сравниваем с и : , значит гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными, т.е. результаты наблюдений можно считать распределенными нормально.

Так как n > 15, применяем критерий 2.

– задаемся доверительной вероятностью P₂ = 0,98 и для уровня значимости q₂ = 1 – P₂ с учетом n = 22 определяем по таблице П8 значения m и P^*. m = 2; P^* = 0,97.

– для вероятности P^* из таблиц для интегральной функции нормированного нормального распределения Ф(t) определяем значение t:

; (11)